
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи для самостоятельного решения. № 1.41. Какое множество имеет большую мощность: а) множество натуральных чисел или множество четных чисел?
№ 1.41. Какое множество имеет большую мощность: а) множество натуральных чисел или множество четных чисел? б) множество четных чисел или множество простых чисел?
№ 1.42 Установить эквивалентность между множеством натуральных чисел N и множеством  .
.
№ 1.43 Показать, что мощность всякого произвольного множества больше или равна мощности всех чисел натурального ряда.
№ 1.44. Установить взаимно-однозначное соответствие между множествами всех рациональных чисел на отрезках (0; 1) и (0;  ).
).
№ 1.45. Установить эквивалентность между множеством всех положительных рациональных чисел и множеством натуральных чисел.
№ 1.46. Задана система числовых множеств:


………………………..
 .
.
Определить мощность множества  .
.
№ 1.47. Является ли множество {(1, 2), (3, 4), (5, 6), (7, 8)} бинарным отношением. Почему?
№ 1.48. Выписать элементы множества {0, 1, 2}´{a,b}. Найти область определения и область значений этого отношения, построить его график.
№ 1.49. Показать на примере, что операция образования декартового произведения не является ни коммутативной, ни ассоциативной.
№ 1.50. Доказать, что декартово произведение дистрибутивно относительно операции объединения, т.е. что для любых множеств А, В и С  .
.
№ 1.51. Пусть b - отношение “есть брат”, j - отношение “есть сестра”. Описать отношения 
№ 1.52. Является ли отношение “быть рядом” транзитивным?
№ 1.53. Задано бинарное отношение на множестве М={1,2,3,4}. Является ли оно рефлексивным, симметричным, антисимметричным, транзитивным? Почему? Найдите область определения dR, область зна-чений rR, обратное отношение R-1, пересечение и объединение R и R-1.
а) R={(1,1), (1,2), (1,3), (2,3), (3,3), (4,1), (4,4)};
б) R={(1,1), (1,2), (2,1), (2,3), (3,2), (3,3), (4,4)};
в) R={(1,1), (1,4), (2,3), (3,2), (4,1)};
г) R={(1,1), (1,2), (1,4), (2,2), (2,3), (3,3), (4,4)};
д) R={(1,1), (1,3), (2,2), (3,3), (4,1), (4,4)};
е) R={(1,1), (1,2), (3,1), (3,2), (3,3), (4,4)};
ж) R={(1,1), (1,2), (2,2), (2,3), (3,4), (4,4)};
з) R={(1,2), (1,3), (2,2), (2,3), (3,3), (4,3)};
и) R={(1,4), (2,3), (3,2), (3,4), (4,1), (4,3)};
к) R={(2,1), (3,1), (3,2), (3,3), (3,4), (4,1)}.
№ 1.54 Найти область определения, область значений, построить график каждого из следующих отношений:
а) 
б) 
в)  и
и 
г) 
д) 
е) 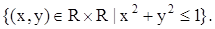
№ 1.55 Доказать, что если:
а) 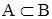 и
и  то
то 
б) 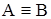 и
и  то
то 
в) 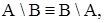 то
то 
№ 1.56. Доказать, что множество всех окружностей (на плоскости), радиусы которых рациональны и центры которых имеют рациональные координаты, есть счетное множество.
№ 1.57. Доказать, что множество всех четырехугольников (на плоскости), вершины которых имеют целые координаты, есть счетное множество.
№ 1.58. Доказать, что множество всех точек плоскости, обе координаты которых есть двоичные дроби, есть счетное множество.
№ 1.59. На улице есть 30 домов, пронумерованных обычным способом: нечетные номера с одной стороны, а четные с другой стороны. Пусть hn обозначает жителя, живущего в доме с номером n. Описать при помощи символов отношение N на множестве жителей такое, что hi находится в отношении N к hj, если они являются соседями.
Как будет выглядеть N, если улица является тупиком?
№ 1.60. Доказать, что любое отношение эквивалентности порождает такое разбиение, что для любых х, у  А или [x]1=[y], или [x]
А или [x]1=[y], или [x] 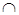 [y]=
[y]= 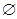 .
.
№ 1.61. Если {A1, A2, … , An} – разбиение А и А конечное, показать, что
 .
.
№ 1.62. Пусть А –произвольное множество и r - отношение на множестве  , определенное следующим образом:
, определенное следующим образом: 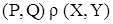 тогда и только тогда, тогда
тогда и только тогда, тогда  . Является ли
. Является ли  отношением порядка?
отношением порядка?
1.63. Докажите справедливость соотношения
 .
.
1.64. Проиллюстрируйте диаграммой Венна следующие разбиения множества I:
а) 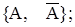
б) 
в) 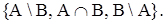
1.65 Каковы свойства соответствия между множеством N натуральных чисел и множеством А степени числа 2:

1.66 Является ли функция f(x)=2x, имеющая тип N®N, отображением, и если – да, то каким? Имеет ли функция f обратную функцию f-1, и если – да , то является ли f-1 отображением?
1.67 Чему равна композиция функций f(x) и g(x), если:
а) f(x)=2x и g(x)=  ;
;
б) f(x)=x3 и g(x)=  ;
;
в) f(x)=2x и g(x)=x+1?
Каковы области определения функций и их композиций?
1.68 Найти композицию преобразований:


 .
.
1.69 Пусть множества b(I), где I={a, b, c} A3 определены следующим образом: b(I) – множество всех подмножеств (булеан) множества I={a, b, c}; А3 – множество всех двоичных векторов длины 3, т.е. А3=В´В´В, где В={0, 1}.
Показать, что между множествами b(I) и А3 имеет место взаимно однозначное соответствие.
№ 1.70. График функции  представляет собой ломанную, звенья которой параллельны координатной оси, либо биссектрисам координатных углов. Координаты каждой вершины ломанной являются целыми числами. Функция
представляет собой ломанную, звенья которой параллельны координатной оси, либо биссектрисам координатных углов. Координаты каждой вершины ломанной являются целыми числами. Функция  определяет отношение Rf на множестве Х=[0, 5]. xRfy
определяет отношение Rf на множестве Х=[0, 5]. xRfy  f(x)=f(y) ( т.е. x
f(x)=f(y) ( т.е. x  y
y  находится в отношении Rf с y
находится в отношении Rf с y  тогда и только тогда, когда f(x)=f(y). Докажите, что Rf –эквива-лентность на Х. Перечислите все классы эквивалентности.
тогда и только тогда, когда f(x)=f(y). Докажите, что Rf –эквива-лентность на Х. Перечислите все классы эквивалентности.
|
|
а) б)
а) б)
|
| ||||
в) г)
|
| ||||
д) е)
|
|
ж) з)
Дата добавления: 2015-02-10; просмотров: 375; Мы поможем в написании вашей работы!; Нарушение авторских прав |






