
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
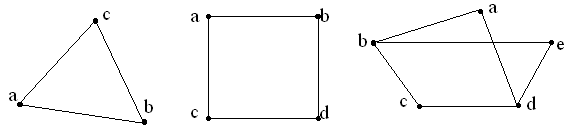
Задачи для самостоятельного решения. № 2.1 Показать, что два графа на рис
№ 2.1 Показать, что два графа на рис. 2.6 изоморфны.
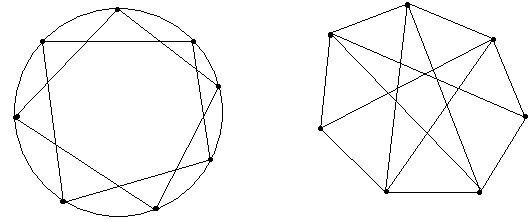
Рис. 2.6
№ 2.2 «Три дома и три колодца». Три поссорившихся соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к колодцу?
№ 2.3 Найти степени и числа вершин для графов пяти правильных многогранников.
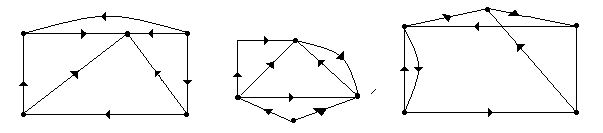
№ 2.4 Для графов, изображенных на рис. 2.7, указать пары, изоморфные друг другу.
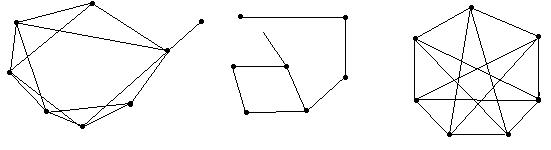
А Б В
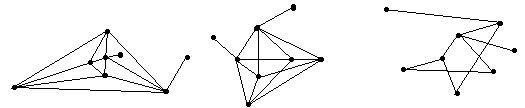 |
Г Д Е
Ж З И
Ж З И
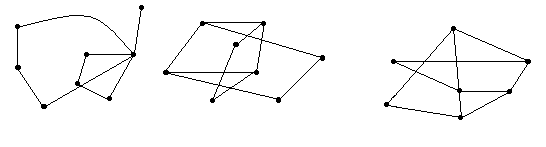 |
К Л М
Рис.2.7
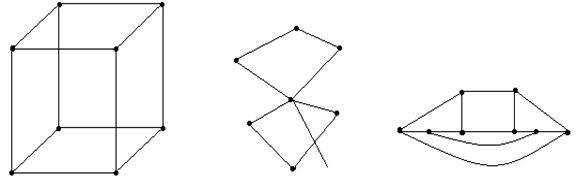
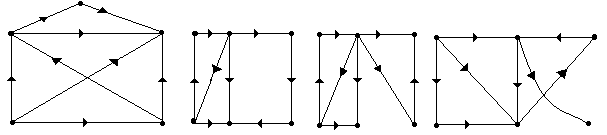
№ 2.5 Среди графов, указанных на рис. 2.8, выделить полные графы (без учета петель).

А Б В Г
Д Е Ж
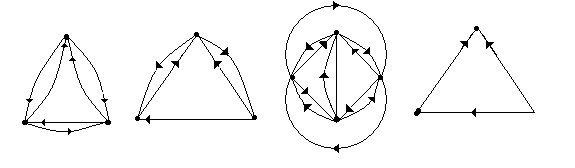
И К Л М
Рис. 2.8
№ 2.6 Дан граф G (Рис. 2.9). Указать, какие из графов, изображенных на рис. 2.9б, являются частями графа G и какие – подграфами.
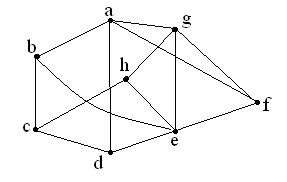 |
Рис. 2.9
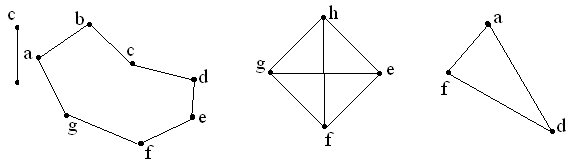
А Б В
Г Д Е
Ж З И

К Л М Н
Рис. 2.9б.
№ 2.8 Какие из графов, приведенных на рис.2.8 и 2.9, являются плоскими?
№ 2.9. Составить матрицы смежности и инцидентности для правильных многогранников.
№ 2.10. Построить матрицы смежности графов, изображенных на рис. 2.9.
№ 2.11 Для заданного на рис. 2.10 (а¸к) графа построить: матрицу смежности, матрицу инциденции, матрицу достижимостей. Найти число внутренней устойчивости. Найти число внешней устойчивости.
А Б В
Г Д Е Ж

З И К
Рис. 2.10.
 |
№ 2.12. Для приведенных на рис. 2.11. графов G1 и G2 найти
 ,
, 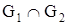 ,
,  .
.
А Б
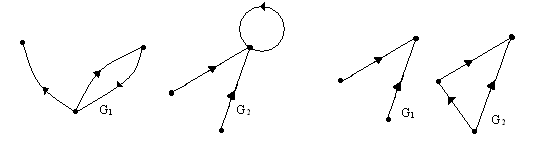
В Г
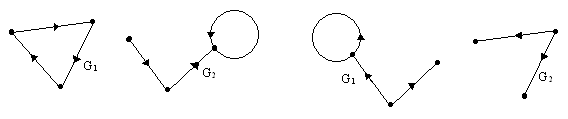
Д Е
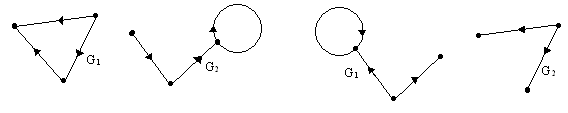
Ж З
Рис. 2.11
№ 2.13. Построить графы, матрицы смежности которых указаны:
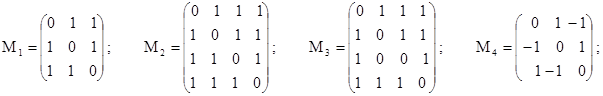
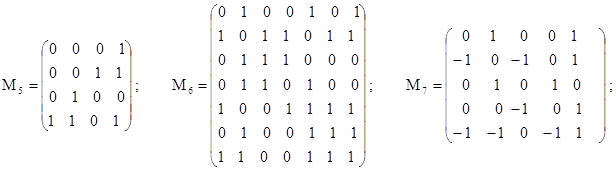

№ 2.14. Построить графы, матрицы инцидентности которых указаны:

 ;
;
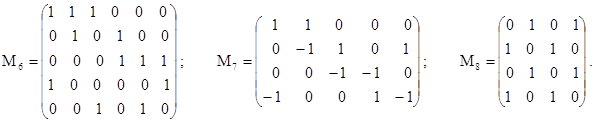
№ 2.15 Груз доставляется из пункта Х0 в пункт Х7 через перевалочные пункты Х0…Х7 (Рис.2.12). Расстояния между пунктами ХiXj указаны на соответствующем графе. Найти путь минимальной длины между Х0 и Х7 и его длину.
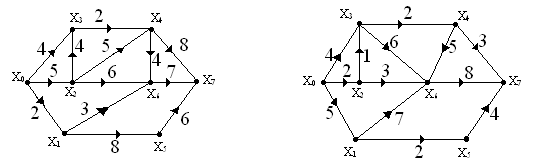
А Б

В Г
Рис. 2.12
№ 2.16 Задан сетевой граф проекта (Рис.2.12). Найти критический путь и минимальное время проекта
Литература
1. Кук Д., Бейз Г. Компьютерная математика. Пер. с англ., М., Мир, 1992 г.
2. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. М., Энергоатомиздат, 1989 г.
3. Ф.А. Новиков. Дискретная математика для программистов. Санкт-Петербург, Питер, 2001 г.
1 Запись [x] означает класс эквивалентности для хÎА.
Дата добавления: 2015-02-10; просмотров: 339; Мы поможем в написании вашей работы!; Нарушение авторских прав |