Координаты центра тяжести тела определяются по формулам

(15)

где 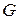– общий вес тела; – координаты точек приложения сил тяжести элементарных частей, на которые разбито тело; – вес элементарной части тела.

Если вес любой элементарной части выразить для объемного тела , для площади – , для линии , где и – соответственно вес единицы объема, площади, длины линии, то получим общие формулы для определения координат центров тяжести однородных объемов

(16)

однородной площади

(17)

и однородной линии

. (18)

В этих формулах – соответственно объем тела, площадь фигуры и длина линии.

Определение координат центров тяжести однородных тел по формулам (16–18) сводится к вычислению определенных интегралов по всему объему, площади или линии. Таким способом получены формулы для определения координат центров тяжести полушара (на расстоянии от основания), конуса (на расстоянии Н от основания), кругового сектора (на расстоянии 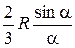от центра круга) и дуги окружности (на расстоянии от центра окружности). Для всех этих объектов центр тяжести расположен на оси симметрии.

Если объемное тело, плоская фигура или линия имеют сложную геометрическую форму, то для определения координат центров тяжести применяются метод разбиения, метод дополнения или метод отрицательных объемов, площадей. В этом случае в формулах (16–18) под и следует понимать соответственно объем, площадь или длину линии отдельных элементов простой геометрической формы (полушар, цилиндр, сектор, треугольник и т.д.), на которые разбита сложная фигура; и – координаты центров тяжести этих элементов в выбранной системе координат.

Координаты центра тяжести плоских фигур (пластин) можно определять также по формулам

, (19)

где – статические моменты площади относительно осей координат.