Сегмент состояния задачи

Состояние процессора, необходимое для восстановления задачи, хранится в системном сегменте, называемом сегментом состояния задачи (Task State Segment - TSS).

Сегмент состояния задачи содержит динамические (обновляемые) и статические (необновляемые) поля. К динамическим относятся поля, соответствующие регистрам общего назначения, сегментным регистрам, регистру флагов, указателю команд EIP, и поле "Связь TSS". Динамические поля автоматически обновляются процессором при сохранении контекста задачи во время переключения на другую задачу. К статическим относятся все остальные поля: селектор LDT, адрес каталога таблиц (PDBR), указатели привилегированных стеков (SS0:SP0, SS1:SP1, SS2:SP2), флаг отладки (T) и базовый адрес карты разрешения ввода-вывода (I/O Permission Map Base Address). Статические поля заполняются системным ПО при создании задачи (при создании TSS) и не изменяются процессором при переключении задач.

Дескриптор TSS должен находиться в GDT. Процессор генерирует нарушение общей защиты при попытке переключиться на задачу, селектор TSS которой содержит бит TI=1. Для запущенной в данный момент задачи (или приостановленной) дескриптор TSS имеет тип "занятый TSS" (S=0, типы 3 и 11). Процессор не поддерживает рекурсию задач, поэтому попытка переключения задач при помощи селектора "занятого TSS" вызывает исключение.

22. Система привилегий программ в ЗРР.

Зачем нужно использовать дескрипторные таблицы двух типов?

В мультизадачной операционной системе можно использовать одну глобальную таблицу дескрипторов для описания областей памяти, принадлежащей операционной системе и несколько локальных таблиц дескрипторов для каждой задачи. В этом случае при соответствующей настройке базовых адресов можно изолировать адресные пространства операционной системы и отдельных задач. Если сделать так, что каждая задача будет пользоваться только своей таблицей дескрипторов, любая задача сможет адресоваться только к своим сегментам памяти, описанным в соответствующей таблице, и к сегментам памяти, описанным в глобальной таблице дескрипторов. В системе может существовать только одна глобальная таблица дескрипторов.

Поле RPL (Requested Privilege Level ) селектора содержит уровень привилегий, запрошенный программой при обращении к сегменту. Программа может обращаться только к таким сегментам, которые имеют соответствующий уровень привилегий. Поэтому программа не может, например, воспользоваться глобальной таблицей дескрипторов для получения доступа к описанным в ней системным сегментам, если она не обладает достаточным уровнем привилегий. На этом основана защита системных данных от разрушения (преднамеренного или в результате программной ошибки) со стороны прикладных программ.

Таблица дескрипторов содержит, помимо базового адреса сегмента, другую информацию, описывающую сегмент (рис. 2.5). Точный формат дескриптора, а также других структур данных и системных регистров, имеющих отношение к работе в защищенном режиме, вы можете найти в 6 томе "Библиотеки системного программиста".

Рис. 2.5. Формат дескриптора сегмента процессора 80286

В частности, дескриптор содержит размер сегмента (предел). При вычислении физического адреса процессор следит за тем, чтобы физический адрес не выходил за пределы, указанные в дескрипторе сегмента. Программа не может обратиться к памяти, лежащей вне пределов, указанных в дескрипторе. Если же она попробует это сделать, ее работа будет прервана. Поэтому, создав, например, сегмент для хранения массива размером 100 байт, вы не сможете записать в него 101 байт или 10 Кбайт данных.

Поле доступа содержит уровень привилегий сегмента и информацию о типе сегмента. Существуют сегменты кода, сегменты данных и системные сегменты. Кроме того, для сегмента кода можно запретить операцию чтения, а для сегмента данных - операцию записи. Поэтому операционная система может создать сегменты кода, которые можно выполнять, но нельзя читать, и сегменты данных, защищенные от записи.

Что же касается привилегий, в процессорах 80ххх и Pentium существуют четыре уровня привилегий - от 0 до 3, причем наибольшие привилегии соответствуют уровню 0. Уровни привилегий часто называют также кольцами защиты (рис. 2.6).

Рис. 2.6. Кольца защиты

В кольце 0 обычно работает ядро операционной системы. Кольцо 1 соответствует уровню привилегий драйверов, кольцо 2 - системам, таким как системы управления базами данных. В наименее привилегированном кольце 3 располагаются прикладные программы, запускаемые пользователем.

Описанная выше схема распределения привилегий может изменяться от одной операционной системы к другой. В операционной системе Windows 3.1 в нулевом кольце располагаются только виртуальные драйверы, все остальные модули Windows, а также приложения, работают в кольце 3.

24. Алгебра логики, определение, аксиомы.

Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Чаще всего предполагается, что высказывания могут быть только истинными или ложными, то есть используется так называемая бинарная или двоичная логика.

Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.

Высказывания строятся над непустым множеством, над элементами которого определены три операции:

•отрицание(унарная операция), обозначение:

Отрицаниев логике – операция над суждениями или высказываниями, результатом которой является суждение «противоположное» исходному. Синоним: логическое "НЕ".

•конъюнкция (бинарная),обозначение:

Конъюнкция— логическая операция, по своему применению максимально приближенная к союзу «и». Синонимы: логическое «И», логическое умножение, иногда просто «И»

•дизъюнкция (бинарная), обозначение: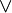

Дизъюнкция- логическое сложение, логическое ИЛИ, включающее ИЛИ; иногда просто ИЛИ — логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу».

Логический ноль 0 и логическая единица 1 — константы.

Аксиомы алгебры логики.

1. ,

2.

3.

4.

5.

6.

7.

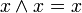
8.

9.

25. Теоремы алгебры логики.

Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Теоремы алгебры логики:

Идемпотентные законы (законы тождества):

Коммутативные законы (переместительные):

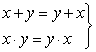
Ассоциативные законы (сочетательные):

Дистрибутивные законы:

Законы отрицания:



Законы двойственности (Теоремы де Моргана):

Закон двойного отрицания:

Законы поглощения (абсорбция):

Операции склеивания:

Операции обобщенного склеивания:

26. Логические функции, область определения логической функции.

Логическая функция (определение учителя) – логическое выражение, состоящее из логических переменных, связанных между собой с помощью операций алгебры логики.

Логическая функция (1) — это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.

Логической функцией F (2) от набора логических переменных х1,…, хn называется функция, которая может принимать только два значения: логический 0 и логическая 1.

Областью определения логической функции n- переменных – называется совокупность точек n- мерного пространства, причём каждая точка создаётся определённой комбинацией значений переменных. (определение учителя).

Область определения логической функции конечна и зависит от количества возможных наборов аргументов. Если n – число аргументов, то количество возможных наборов аргументов равно 2n.

Множество значений функции F(x1,…, xn) – это множество {0,1}, т. е. F=0 либо 1.

Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записываются наборы аргументов, а в правой – соответствующие значения функции.