Минимизации функций

Для начала вам надо уметь составлять СДНФ и СКНФ, потому что это, скорее всего, тоже будет в контрольной. Что это такое можно прочитать и в материалах, и в других доступных источниках. Если кратко, то СКНФ - совершенно конъюнктивная нормальная форма, а СДНФ - совершенно дизъюнктивная нормальная форма.

Совершенно конъюнктивная НФ - конъюнкция дизъюнкций, причём в каждой дизъюнкции (в каждой скобке) присутствуют все переменные, входящие в формулу, либо их отрицание, нет одинаковых дизъюнкций, в каждой дизъюнкции нет одинаковых слагаемых:

СКНФ:

Совершенно дизьюнктивная НФ - дизьюнкция коньюнкций , причём в каждой коньюнкции присутствуют все переменные, входящие в формулу, либо их отрицание, нет одинаковых коньюнкций, в каждой коньюнкции нет одинаковых слагаемых:

СДНФ:

Теперь рассмотрим пример, в котором по таблице истинности построим СДНФ и СКНФ, а затем уже перейдём к минимизации.

Для примера возьмём функцию с тремя переменными и уже разобранную на занятии.

Рассмотрим по пунктам, как составить СДНФ:

1. Записываем произведение наборов переменных , если функция равна 1 (F=1);

2. Берём переменную с отрицанием, если её значение равно 0

3. Между каждым произведением набора переменных ставим знак логического сложения

Теперь составим СДНФ для нашей таблицы истинности.

СДНФ:

Рассмотрим по пунктам, как составить СКНФ:

1. Записываем произведение наборов переменных , если функция равна 0 (F=0);

2. Берём переменную с отрицанием, если её значение равно 1 ;

3. Между каждым произведением набора переменных ставим знак логического сложения

Составим СКНФ для таблицы истинности.

СКНФ:

Теперь перейдём к минимизации функций.

Сначала рассмотрим способ, с помощью которого мы будет упрощать СДНФ и СКНФ. Начнём с СДНФ:

Теперь ищем пары слагаемых, которые отличаются только одной переменной, то есть в одном случае она с отрицанием, в другом – без. Выделяем такие пары (тут такие пары будут выделены одинаковыми цветами) :

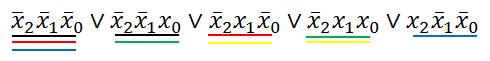
Но стоит заметить, что если разбить слогаемые на пары, то одно из слогаемых останется без пары. И тут мы обращаемся к аксиомам алгебры логики: Исходя из этого, делаем следующие преобразования:

Теперь делим слогаемые на пары и выносим за скобки одинаковые переменные, после чего содержимое скобок сокращаются (как и почему это происходит, вы должны знать):

Теперь перейдём к минимизации СКНФ. Принцип такой же, как и с СДНФ:

Скорее всего контрольная у нас будет по СДНФ, но к СКНФ тоже надо быть готовым. А теперь то, что точно будет в контрольной. Карты Карно – ещё один способ минимизации.

Работать будем уже с имеющейся у нас таблицей истинности. Для начала рисуем такую таблицу:

Отдельно нужно отметить нумерацию внутри таблицы. Это вам стоит запомнить.

Теперь заполняем таблицу. Соответствующие клетки заполняем 1, если F=1, и оставляем пустыми либо ставим 0, если F=0:

Теперь ищем группы соседних 1, которые зацикливаются. Соседними являются 1, стояие рядом друг с другом по горизонтали и по вертикали. Так же соседними являются крайние 1, то есть 1 из клетки 0 являяется соседней с 1 из клетки 2. Если трудно понять, что значит «зацикливаются», то можете запомнить, что группы единиц могут состоять из 2, 4, 8 и любому другому колличеству единиц равному 2 в степени n. А зациклиться такие группы могут только в квадрате или прямоугольнике. Так же в разные группы, при необходимости, могут попадать одни и теже 1. В конце я рассмотрю её пару отдельных случаев, а пока вернёмся к примеру. Итак, выделяем группы:

Пусть группа, выделенная чёрным, будет группой 1, а выделенная красным – группой 2. Смотрим в группах переменные, которые остаются неизменными. В группе 1 это x2, а в группе два – x1 и x0. Теперь смотрим, какие значения у этих переменных: если 0, то берём переменную с отрицание, если 1, то без. И у нас получается следующее уравнение:

Теперь ещё немного о картах Карно. У нас в контрольных будут функции с тремя и четырьмя переменными, так что вот таблица для четырёх переменных, её нужно обязательно запомнить, особенно нумерацию.

А сейчас на такой таблице рассмотрим ещё два случая, связанных с группами из 1:

Тут почти все 1 отнесенны к группам. Остальсь только 1 из клеток 14 и 8. Сначала посмотрим на 1 в клетке 14. Она соседня с 1 из клеток 6 и 10. Но, как мы уще знаем, нельзя делать группу из трёх 1. Следовательно, можно объеденить ту 1 в группу с 1 либо из клетки 6, либо из клетки 10. И то, и то будет верно. Но нельзя объединять 1 и с 1 из клетки 6, и из клетки 10. То есть либо так:

Осталась 1 в клетке 8. Тут всё просто. Если 1 не с кем зациклить, то она зацикливается сама на себе. Выглядеть это будет так:

Ну, вроде, всё. Будут вопросы, обращайтесь. Успехов всем на контрольной!