
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Процесс коммутации токов в фазах питающего трансформатора ТП при переключении вентилей.
Индуктивные сопротивления обмоток трансформатора, обусловленные потоками рассеяния в магнитной системе, определяются из опыта короткого замыкания трансформатора, и в расчетах учитываются в виде общей индуктивности Ls, представляющей собой суммарную индуктивность рассеяния вторичной обмотки и, приведенную к ней, индуктивность первичной обмотки. Влияние на процесс коммутации активных сопротивлений обмоток трансформатора учитывать не будем из-за незначительности этого влияния. По-прежнему выпрямленный ток считаем идеально сглаженным (wLн =¥).
Индуктивные сопротивления обмоток учтены введением в схему индуктивностей Ls . Предположим, что в проводящем состоянии находится вентиль VS1 . В момент Q1 поступает включающий импульс на вентиль VS2 . Поскольку потенциал анода вентиля в этот момент положителен относительно катода, вентиль включается.
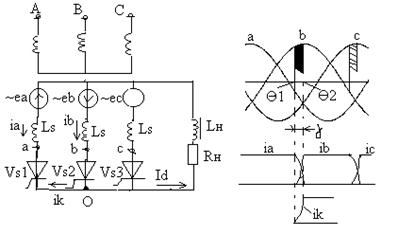
Начиная с момента Q1 оба тиристора включены и две фазы (“а” и “b”) вторичной обмотки трансформатора оказываются замкнутыми через них накоротко. Под воздействием ЭДС обмоток этих фаз (eа и eb) в короткозамкнутой цепи (контура коммутации) появляется ток короткого замыкания ik , который является коммутирующим током.
Этот ток можно в любой момент интервала коммутации (Q2 - Q1 ) определить по формуле:
ik = (U2m/2Xs)*{cos a - cos (a + Q)} (3-7)
где U2m -амплитудное значение линейного напряжения между фазами “a” и “b”.
Xs= wLS (3-8) a - угол управления.
Учитывая, что выпрямленный ток Id при wLн = ¥ в интервале коммутации остается неизменным, можно, согласно первому закону Кирхгофа для точки 0 записать:
ia + ib + Id = 0 ;
или с учетом направления токов: ia + ib = Id = const.
Последнее уравнение справедливо для любого момента интервала коммутации. Пока ток проводит только вентиль VS1 , получаем ia = Id и ib = 0. На интервале одновременной проводимости вентилей VS1 и VS2 (интервал коммутации тока с фазы “а” на фазу “b”):
ia = Id - ik и ib = ik. Когда коммутация закончится и ток будет проводить только вентиль VS2 , получим: ib = Id ; ia = 0.
Из рис 16 видно, что в интервале от Q1 до Q2 ток ib плавно увеличивается, а ia уменьшается. Когда ток ib станет равным Id , а ток ia снизится до нуля, вентиль VS1 выключится и ток нагрузки будет продолжать протекать только через вентиль VS2 .
Длительность интервала коммутации характеризуется углом коммутации g, который может быть определен из следующего уравнения (для трехфазной нулевой и трехфазной мостовой схем):
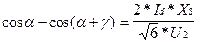
обозначив угол коммутации g при угле управления a = 0 через g0, можно записать:

Подставляя в исходное уравнение значение g0, получаем:
g = arccos {cos a + cos g0 - 1} - a .
С учетом действия ЭДС самоиндукции мгновенное значение выпрямленного напряжения на интервале коммутации тока равно полусумме ЭДС коммутируемых фаз.
Ud = (Ua + Ub)/2 . (3-12)
где Ua и Ub - мгновенные значения фазных напряжений вторичной обмотки трансформатора.
Так как, в зоне коммутации мгновенное значение выпрямленного напряжения снижается, по сравнению с мгновенной коммутацией, до величины Ud , происходит уменьшение среднего значения выпрямленного напряжения. Его величина определяется выражением:
 (3-14)
(3-14)
Из (3-7), (3-8), и (3-14) можно получить:  (3-15)
(3-15)
Дата добавления: 2015-02-10; просмотров: 408; Мы поможем в написании вашей работы!; Нарушение авторских прав |