Построение эпюр для сложных балок, рам и криволинейных брусьев

Под сложной понимается балка, опирающаяся более чем на две опоры, имеющая в своем составе врезанные шарниры (рисунок 5.1).

При решении сложных балок необходимо составить дополнительные уравнения в виде уравнений моментов относительно врезанного шарнира для одной из частей балки, а при построении эпюр моментов необходимо учесть то, что в данном сечении с врезанным шарниром момент должен иметь нулевую ординату.

Рамой называется система, состоящая из прямолинейных стержней, соединенных жесткими узлами (рисунок 5.2).

Построение эпюр для рам выполняется также, как для балок, но с учетом следующих особенностей:

1. для рамы строится не две, а три эпюры – продольной, поперечной сил (N и Q) и изгибающего момента (M);

2. для эпюр N и Q принимаются такие же правила знаков как для балок, но при построении эпюр положительные ординаты откладываются снаружи рамы, а отрицательные – внутри ее;

3. правила знаков для изгибающего момента принимаются условно, например, против часовой стрелки «+», против часовой стрелки «–», но, несмотря на это, сама эпюра строится на растянутом или сжатом волокне без указания знака;

4. построенные эпюры N, Q и M проверяются путем вырезания узлов и проверки их равновесия под действием внутренних силовых факторов и внешних нагрузок (если равновесие узла обеспечивается – эпюра построена правильно!).

При построении эпюр для криволинейных стержней, например арок, все уравнения В.С.Ф. составляются в угловых координатах, то есть через переменный угол, тогда получаемые эпюры также будут иметь криволинейные очертания (рисунок 5.3).

§6. Напряжение. Интегральные уравнения равновесия (И.У.Р.)

В курсе сопротивления материалов кроме понятия В.С.Ф. встречается понятие, называемое напряжением. Напряжение – это мера, характеризующая интенсивность распределения В.С.Ф. по сечению нагруженного бруса.

Покажем эту меру в рассматриваемом сечении некоторого бруса (рисунок 6.1).

DА – элементарная площадь;

– элементарное внутреннее усилие, действующее по элементарной площади.

Отношение элементарного усилия к элементарной площади представляет собой среднее напряжение, действующее по элементарной площади.

(6.1)

Переходя к пределу, получим точное напряжение в точке данной элементарной площади:

(6.2)*

В расчетах удобнее использовать полное напряжение в виде проекций по осям координат. Для этого напряжение проецируют по трем главным центральным осям сечения. В итоге получают одну нормальную и две касательные составляющие (рисунок 6.2).

s_z – нормальное напряжение, t_zx и t_zy – касательные напряжения.

Таким образом, полное напряжение можно представить следующей суммой:

Между тремя составляющими полного напряжения и шестью внутренними силовыми факторами существуют зависимости , для получения которых рассмотрим следующий рисунок (рисунок 6.3).

Учитывая, что брус находится в равновесии, можно составить следующие зависимости:

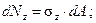
это элементарная продольная сила, тогда полная продольная сила найдется как сумма (или интеграл) вида:

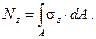
Аналогично можно получить и остальные силовые факторы:

Система уравнений (6.4) называется интегральными уравнениями равновесия.

С помощью этой системы можно определить какой-либо фактор через одно из напряжений.

Для решения обратных задач (что требуется чаще), то есть для определения какого-либо напряжения через соответствующий внутренний силовой фактор, необходимо знать закон изменения искомого напряжения по сечению бруса. Для этого необходимо провести совместный анализ напряженного и деформированного состояния (Н.Д.С.)

§7. Деформации и перемещения. Деформированное состояние в точке (Д.С.Т.)

Известно, что свойством любого тела является способность деформироваться, то есть изменять свою форму и размеры.

В курсе сопротивления материалов различают деформации упругие и классические, линейные и угловые, абсолютные и относительные. Кроме того, при деформировании тела в нем возникает перемещение, то есть происходит изменении местоположения точек по отношению к их исходному положению. Перемещения также могут быть линейными и угловыми.

Рассмотрим два отрезка ab и ac в плоскости XOY в реальном теле до и после его деформирования (рисунок 7.1).

dx, dy – длина отрезков ab и ac до деформации;

Ddx, Ddy – приращения отрезков ab и ac соответственно, то есть абсолютные линейные их (отрезков) деформации ( [м] ).

– абсолютная угловая деформация (угол сдвига в плоскости xy);

– линейные перемещения точек a, b и c соответственно;

a и b – условные перемещения.

Если провести аналогичные рассуждения, выбрав третью ось z, получим еще три составляющих деформации: e_z, g_xz, g_yz. Тогда с применением шести составляющих деформации можно выполнить полное описание деформируемого состояния в точке.

Таким образом, совокупность трех линейных деформаций по направлениям и трех угловых деформаций по плоскостям, проходящим через данную точку, представляют собой деформированное состояние точки.

Под деформацией будет пониматься либо процесс изменения формы или размеров тела, либо какой-либо вид нагружения. В последнем случае различают следующие виды деформации: растяжение или сжатие, сдвиг или срез, кручение, изгиб, сложное сопротивление.

Первые четыре вида деформации называются простыми, а их сочетание представляет собой сложное сопротивление.

Для каждой деформации будет характерна своя совокупность составляющей деформации согласно системы (7.1).

В дальнейшем будем рассматривать по отдельности все названные виды деформаций.

§8. Основные гипотезы о деформируемом теле. (Гипотезы сопротивления материалов)

При решении задач курса сопротивления материалов не всегда удается учесть все факторы нагружения или свойства материала в виду того, что это представляет большие трудности. В этом случае принимается ряд допущений, или гипотез, которые упрощают анализ выполняемого расчета. Возникающие при этом неточности или погрешности не превышают допустимых пределов, характерных для инженерного расчета.

d < 10% (погрешность не превышает 10%)

В курсе сопротивления материалов довольно часто используют следующие гипотезы, характеризующие как свойства деформируемого материала, так и особенности его нагружения. Рассмотрим эти гипотезы.

1. Гипотеза о сплошности материала предполагает, что материал заполняет объем тела без пустот или посторонних включений.

2. Гипотеза об однородности и изотропности предполагает, что свойства материала одинаковы во всех точках и по всем направлениям в теле.

3. Гипотеза об идеальной упругости материалов предполагает, что материал является абсолютно упругим, то есть в нем не остаются деформации после снятия внешнего нагружения.

4. Гипотеза о линейной зависимости между нагрузками и деформациями в теле предполагает, что с изменением нагрузки пропорционально изменяется и деформация, то есть считается справедливым закон Гука (F = – k×x).

5. Гипотеза о малости деформаций предполагает, что деформации в теле намного меньше, чем его абсолютные размеры (рисунок 8.1).

6. Принцип суперпозиции (принцип независимости действия сил) предполагает, что результат действия группы сил равен сумме результатов действия каждой силы в отдельности (рисунок 8.2).