Задание К1

Точка В движется в плоскости ху (рис. К1.0-К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f₁ (t), у = f₂ (t), где х и у выражены в сантиметрах, t -в секундах.

Найти уравнение траектории точки; для момента времени t₁, = 1с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Зависимость х = f₁, (t) указана непосредственно на рисунках, а зависимость у = f₂ (t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7-9 в столбце 4). Как и в задаче C1 номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 - по последней.

Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются касательное и нормальное ускорения точки.

Таблица К1

Номер условия	y = f2(t)
Рис. 0-2	Рис.3-6	Рис.7-9

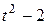
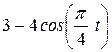
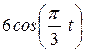
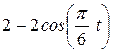
В данной задаче все искомые величины нужно определить только для момента времени t₁ = 1 с. В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы: cos 2a= 1 - 2sin²a = 2 cos²a- 1; sin 2a = 2sin a×cos a.