
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 8. Найти амплитуду А и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний
Найти амплитуду А и начальную фазу  гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями х1 = х1(t) и х2 = х2(t). Написать уравнение результирующего колебания.
гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями х1 = х1(t) и х2 = х2(t). Написать уравнение результирующего колебания.
| Вариант | х1 = х1(t), см | х2 = х2(t), см |
х1 = 4 cos( 2pt +  ) )
| х2 = 3 cos( 2pt +  ) )
| |
х1 = 2 cos( pt +  ) )
| х2 = 1 cos( pt +  ) )
| |
х1 = 3 cos( 3pt +  ) )
| х2 = 6 cos( 3pt +  ) )
| |
х1 = 1,5 cos( pt +  ) )
| х2 = 4,5 cos( pt +  ) )
| |
х1 = 2,5 cos( 4pt +  ) )
| х2 = 5 cos( 4pt +  ) )
| |
х1 = 3,5 cos(  t + t +  ) )
| х2 = 1 cos(  t + t +  ) )
| |
х1 = 1 cos( 2pt +  ) )
| х2 = 3,5 cos( 2pt+  ) )
| |
х1 = 5 cos( pt +  ) )
| х2 = 2,5 cos( pt +  ) )
| |
х1 = 4,5 cos( 2pt +  ) )
| х2 = 1,5 cos( 2pt +  ) )
| |
х1 = 6 cos( 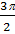 t + t +  ) )
| х2 = 2,6 cos( 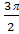 t + t +  ) )
|
Пример 1.Движение материальной точки массой 10 кг задано уравнением 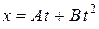 , где А= 4 м/с, В = – 0,05 м/с2. Определить момент времени, в который скорость u точки равна нулю. Найти координату и ускорение в этот момент. Вычислите перемещение точки и значение силы, действующей на точку в этот момент.
, где А= 4 м/с, В = – 0,05 м/с2. Определить момент времени, в который скорость u точки равна нулю. Найти координату и ускорение в этот момент. Вычислите перемещение точки и значение силы, действующей на точку в этот момент.
Дано: 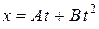 ;
; 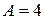 м/с;
м/с;  – 0,05 м/с2.
– 0,05 м/с2.
Найти: 1) t 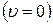 ; 2) x; 3) a; 4) Dr; 5) F.
; 2) x; 3) a; 4) Dr; 5) F.
Решение:Материальная точка совершает одномерное, прямолинейное движение вдоль оси x, уравнение которого имеет вид:

Мгновенная скорость материальной точки – есть первая производная от координаты по времени
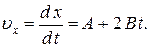
Определим момент времени t, в который скорость точки равна нулю:
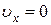 ,
,
 ,
,
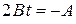 ,
,
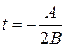 .
.
Подставим числовые значения
 с.
с.
Определим координату в момент времени t= 40 c:
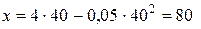 м.
м.
Перемещение точки Drх = х – х0. Drх = 80 – 0 = 80 м. х0 = 0 – координата точки в момент времени t0 = 0. Dr = 80 м.
Мгновенное ускорение материальной точки – есть первая производная от проекции скорости на ось x по времени
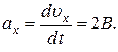
Выполним вычисления:
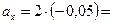 – 0,1 м/с2; а = 0,1 м/с2.
– 0,1 м/с2; а = 0,1 м/с2.
Сила определяется по второму закону Ньютона: F = ma. Вычислим значение силы F = 10×0,1 = 1 Н.
Ответ:t = 40 c; x = 80 м;а = 0,1 м/с2; Dr = 80 м; F = 1Н.
Пример 2. Диск радиусом r = 20 см вращается согласно уравнению 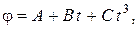 где
где 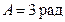 ;
; 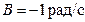 ;
; 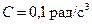 . Определить тангенциальное
. Определить тангенциальное  , нормальное
, нормальное 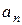 и полное a ускорения точек на окружности диска для момента времени
и полное a ускорения точек на окружности диска для момента времени 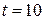 с.
с.
Дано: 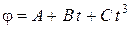 ;
; 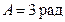 ;
; 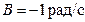 ;
; 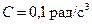 ;
; 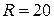 см = 0,2 м ;
см = 0,2 м ; 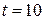 с.
с.
Найти: 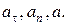
Решение:В задаче дано уравнение движения диска в проекции на ось вращения
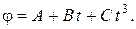
Угловая скорость диска
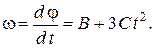
Угловое ускорение диска
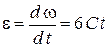 .
.
Связь между линейной и угловой скоростями
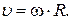
Тогда линейная скорость диска
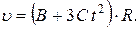
Выполним вычисления 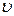 для момента времени
для момента времени 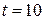 с:
с:
u =( – 1+3·0,1·102)·0,2 = 5,8 м/с.
Связь между тангенциальным  и угловым ускорениями e
и угловым ускорениями e
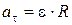 .
.
Тогда 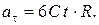
Выполним вычисления 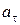 для момента времени
для момента времени 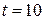 с:
с:
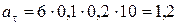 м/с2.
м/с2.
Модуль нормальной составляющей ускорения
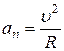 .
.
Произведем вычисления 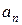 :
:
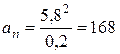 м/с2.
м/с2.
Модуль полного ускорения a
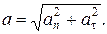
Выполним вычисления а:
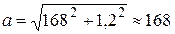 м/с2.
м/с2.
Ответ: 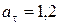 м/с2 ;
м/с2 ; 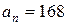 м/с2;
м/с2; 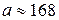 м/с2.
м/с2.
Пример 3. Горизонтальная платформа массой 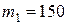 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой
кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 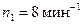 . Человек массой
. Человек массой 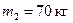 стоит при этом на краю платформы. С какой угловой скоростью
стоит при этом на краю платформы. С какой угловой скоростью 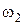 начнёт вращаться платформа, если человек перейдёт от края платформы к её центру? Считать платформу круглым однородным диском, а человека – материальной точкой.
начнёт вращаться платформа, если человек перейдёт от края платформы к её центру? Считать платформу круглым однородным диском, а человека – материальной точкой.
 Дано:
Дано: 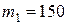 кг;
кг; 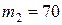 кг;
кг;  мин –1=
мин –1=  с –1.
с –1.
Найти: 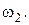
Решение: Воспользуемся законом сохранения момента импульса относительно оси Z: 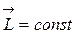 или
или 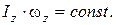
Рассмотрим два случая:
а) человек на краю платформы
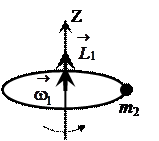

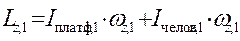 , где
, где 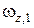 – угловая скорость платформы и человека в первом случае.
– угловая скорость платформы и человека в первом случае.
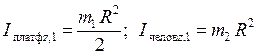 , где R – радиус платформы.
, где R – радиус платформы.
 б)человек в центре платформы
б)человек в центре платформы
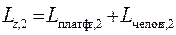
 , где
, где 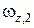 – угловая скорость платформы и человека, после того как он перешёл в центр платформы.
– угловая скорость платформы и человека, после того как он перешёл в центр платформы.
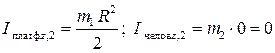
Согласно закону сохранения момента импульса 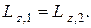
Тогда
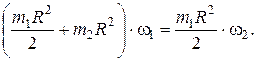
Сократим на 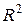 и учтём, что
и учтём, что 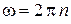 :
:

Выразим 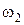
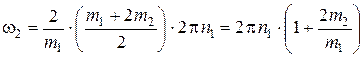 .
.
Выполним вычисления:
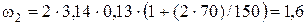 рад/с2.
рад/с2.
Ответ:  рад/с2.
рад/с2.
Пример 4.Кислород массой m = 2 кг занимает объем V1 = 1 м3 и находится под давлением р1 = 0,15 МПа. При нагревании газ расширился при постоянном давлении до объема V2 = 1,3 м3, а затем его давление возросло до р3 = 0,21 МПа при неизменном объеме. Найти изменение внутренней энергии 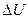 газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса в осях (р;V).
газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса в осях (р;V).
Дано: m = 2 кг; М = 0,032 кг/моль; V1 = 1 м3, V2 = V3 = 1,3 м3;
р1 = р2 = 0,15 МПа, р3 = 0,21 МПа.
Найти: 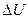 ,
, 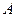 ,
,  .
.
Решение. Изменение внутренней энергии газа выражается формулой
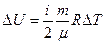 .
.
В данном случае 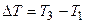 .
.  , (1)
, (1)
где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5 ).
Температуры газа в каждом состоянии найдем, используя уравнение Менделеева – Клапейрона
 .
.
Отсюда 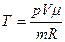 .
.
Подставим численные значения параметров каждого из трех состояний
Т1 = 289 К;
Т2 = 375 К;
Т3 = 526 К.
Подставляя в выражение (1) числовые значения находим
DU = 307,7 кДж.
Работа расширения газа при постоянном давлении выражается формулой A = p(V2 – V1). Используя уравнениеМенделеева – Клапейрона, получим 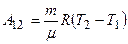 .
.
Работа газа при  равна нулю.
равна нулю.
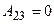 .
.
Таким образом, полная работа, совершаемая газом, равна
А = А12 = 44,7 кДж.
Согласно первому началу термодинамики теплота Q, переданная газу, равна сумме изменения внутренней энергии 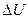 и работы А:
и работы А: 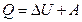 , следовательно,
, следовательно,
Q = 307,7 кДж + 44,7 кДж = 352,4 кДж = 0,35 МДж.
График процесса в осях (p;V) приведен на рисунке.
 р, МПа
р, МПа


 0,21 3
0,21 3
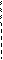



 0,15 1 2
0,15 1 2
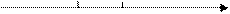 |
0 1 1,3 V, м3
Пример 5. Электрическое поле создано зарядами 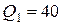 нКл и
нКл и 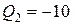 нКл, находящимися на расстоянии 10 см. Определить напряжённость и потенциал поля в точке, удалённой от первого заряда на 12 см, а от второго на 6 см.
нКл, находящимися на расстоянии 10 см. Определить напряжённость и потенциал поля в точке, удалённой от первого заряда на 12 см, а от второго на 6 см.
Дано: 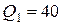 нКл =
нКл = 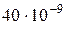 Кл;
Кл; 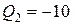 нКл =
нКл = 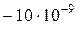 Кл;
Кл;
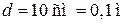 ;
; 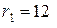 см = 0,12 м;
см = 0,12 м; 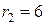 см = 0,6 м.
см = 0,6 м.
Найти: 
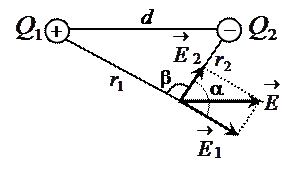
Решение: В соответствии с условием задачи изобразим вектора напряжённостей, созданные зарядами Q1 и Q2 в точке А (рис.):
 |
А
Рис.
Согласно принципу суперпозиции
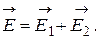
Используя теорему косинусов, перейдём от векторной формы к скалярной:
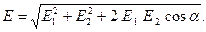 (1)
(1)
Напряжённость электрического поля, создаваемого точечными зарядами 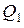 и
и 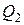 на расстояниях
на расстояниях  и
и 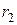 , соответственно равны:
, соответственно равны:
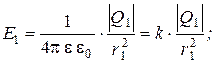
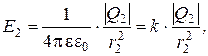
так как 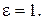
Определим значение 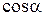 из треугольника со сторонами
из треугольника со сторонами 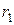 ,
, 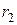 , d, используя теорему косинусов (рис.):
, d, используя теорему косинусов (рис.):

Таким образом,
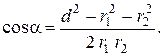
Произведём расчёт  :
:
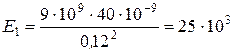 Н/Кл,
Н/Кл,
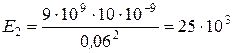 Н/Кл.
Н/Кл.

Для расчёта результирующего значения напряжённости Е подставим значения 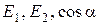 в формулу (1):
в формулу (1):
 Н/Кл.
Н/Кл.
Так как поле создаётся двумя точечными зарядами, то потенциал в рассматриваемой точке следует искать методом суперпозиции. В соответствии с этим
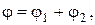
где  – потенциалы в рассматриваемой точке, созданные зарядами
– потенциалы в рассматриваемой точке, созданные зарядами 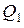 и
и 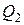 соответственно.
соответственно.
Используя формулу потенциала поля, создаваемого точечным зарядом, получим:

Выполним вычисления:
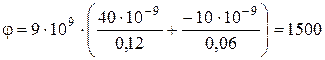 В.
В.
Ответ:  Н/Кл,
Н/Кл,  =1500 В.
=1500 В.
Пример 6. Три источника тока с ЭДС  В,
В, 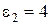 В,
В, 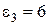 В и внутренними сопротивлениями
В и внутренними сопротивлениями 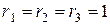 Ом и три реостата с сопротивлениями
Ом и три реостата с сопротивлениями 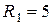 Ом,
Ом,  Ом,
Ом, 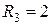 Ом соединены, как показано на рисунке. Определить силу тока в реостатах.
Ом соединены, как показано на рисунке. Определить силу тока в реостатах.
Дано:  В;
В; 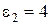 В;
В; 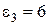 В;
В; 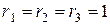 Ом;
Ом; 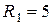 Ом;
Ом;
 Ом;
Ом; 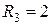 Ом.
Ом.
Найти: 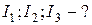
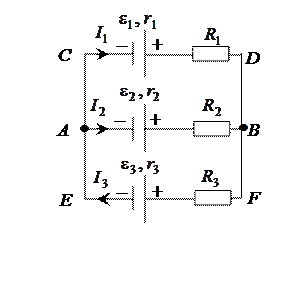 Решение:
Решение:
Рис.
Силы токов в разветвленной цепи можно определить с помощью правил Кирхгофа. Для этого необходимо составить три уравнения. Перед составлением уравнений необходимо:
а) выбрать произвольно направления токов, текущих через сопротивления, указав их стрелками на чертеже;
б) выбрать направления обхода контуров.
В нашем случае направление токов выберем как на рисунке и обходы контуров по часовой стрелке.
Воспользуемся первым правилом Кирхгофа, учитывая что, ток подходящий к узлу входит в уравнение со знаком “+”, а ток отходящий из узла – со знаком “–” .
Для узла А
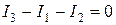 ,
,
или
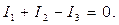 (1)
(1)
При составлении уравнений по второму правилу Кирхгофа учитываем следующие правила знаков:
1) если ток по направлению совпадает с выбранным направлением
обхода контуров, то соответствующее произведение  входит в уравнение со знаком “плюс”, иначе – со знаком “минус”;
входит в уравнение со знаком “плюс”, иначе – со знаком “минус”;
2) если при обходе контура приходится идти от “–” к “+” внутри
источника тока, то соответствующая 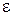 входит в уравнение со знаком “плюс”, иначе – со знаком “минус”.
входит в уравнение со знаком “плюс”, иначе – со знаком “минус”.
Для контуров
1) ACDBА:
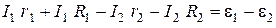 , (2)
, (2)
2) CDFEС:
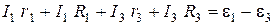 . (3)
. (3)
Подставив значения 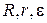 в соотношения (1), (2) и (3), получим систему уравнений:
в соотношения (1), (2) и (3), получим систему уравнений:
 .
.
Решим эту систему с помощью определителей. Для этого запишем её в виде:

Искомые токи найдем по формулам:
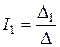 ;
;  ;
; 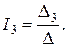
Найдем определители 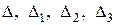 :
:

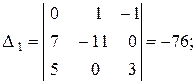
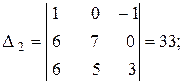
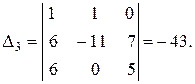
Таким образом
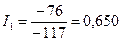 А;
А; 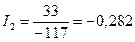 А;
А; 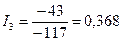 А.
А.
Знак “минус” у тока 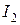 говорит о том, что направление тока на рисунке было указано противоположно истинному, т.е. ток идет от узла B к узлу A.
говорит о том, что направление тока на рисунке было указано противоположно истинному, т.е. ток идет от узла B к узлу A.
Ответ: 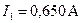 ;
; 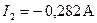 ;
; 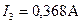 .
.
Пример 7. Два параллельных бесконечно длинных провода, по которым текут токи I1 = I2 = 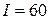 А одного направления, расположены на расстоянии
А одного направления, расположены на расстоянии 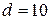 см друг от друга в вакууме. Определить индукцию магнитного поля в точке, отстоящей от одного проводника на расстояние
см друг от друга в вакууме. Определить индукцию магнитного поля в точке, отстоящей от одного проводника на расстояние 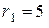 см и от другого на
см и от другого на 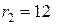 см.
см.
Дано: 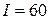 А;
А; 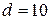 см = 0,1 м;
см = 0,1 м; 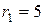 см = 0,05 м;
см = 0,05 м;
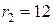 см = 0,12 м.
см = 0,12 м.
Найти: B.
Решение: Для нахождения индукции магнитного поля  в указанной точке А (рис.) определим направления векторов индукций
в указанной точке А (рис.) определим направления векторов индукций 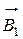 и
и 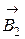 полей, создаваемыхкаждым проводником в отдельности, и сложим их геометрически (по правилу параллелограмма):
полей, создаваемыхкаждым проводником в отдельности, и сложим их геометрически (по правилу параллелограмма):
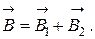
Сделаем рисунок. Выберем направление токов в проводниках «от нас» Ä. Направление векторов 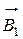 и
и 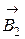 определяем по правилу правого винта (правило правой руки): вращая винт с правой нарезкой по направлению линии магнитной индукции, его поступательное движение укажет направление силы тока.
определяем по правилу правого винта (правило правой руки): вращая винт с правой нарезкой по направлению линии магнитной индукции, его поступательное движение укажет направление силы тока.

I1 I2
Рис.
Абсолютное значение индукции В найдём по теореме косинусов:
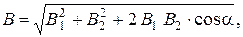 (1)
(1)
где 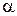 – угол между векторами
– угол между векторами 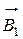 и
и 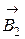 , равный углу между радиус–векторами
, равный углу между радиус–векторами 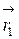 и
и 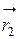 , как углы со взаимно перпендикулярными сторонами.
, как углы со взаимно перпендикулярными сторонами.
Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током определяется формулой:
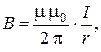
где 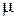 = 1 (среда – вакуум).
= 1 (среда – вакуум).
Тогда от двух рассматриваемых проводников магнитные индукции соответственно  равны:
равны:
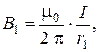 и
и 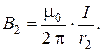
Подставляя значения 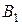 и
и 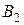 в формулу (1) и вынося
в формулу (1) и вынося 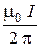 за знак корня, получим:
за знак корня, получим:
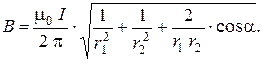 (2)
(2)
Вычислим  , используя, что
, используя, что 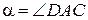 . Согласно теореме косинусов запишем:
. Согласно теореме косинусов запишем:

Отсюда
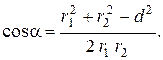
Подставляя данные, вычислим значение  :
:
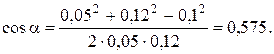
Вычислим согласно формуле (2) магнитную индукцию поля в точке А:
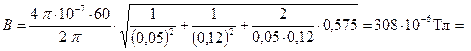 =308мкТл.
=308мкТл.
Ответ: 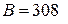 мкТл.
мкТл.
Пример 8. Складываются два колебания одинакового направления, выражаемых уравнениями 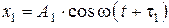 ,
, 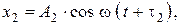 где
где 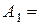 1 см,
1 см, 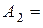 2 см,
2 см, 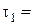 1/6 с,
1/6 с,  1/2 с,
1/2 с, 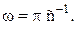 Определить:
Определить:
1) начальные фазы составляющих колебаний;
2) амплитуду и начальную фазу результирующего колебания;
3) записать уравнение результирующего колебания.
Дано: 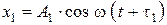 ;
;  ;
;
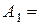 1 см = 0,01 м;
1 см = 0,01 м;  2 см = 0,02 м;
2 см = 0,02 м; 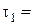 1/6 с;
1/6 с;  1/2 с;
1/2 с;  .
.
Найти: 1) 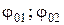 ; 2) А, j0; 3) х = х(t).
; 2) А, j0; 3) х = х(t).
Решение: 1) Уравнение гармонического колебания
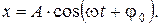 (1)
(1)
Для данных гармонических колебаний:
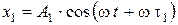 , (2)
, (2)
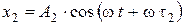 . (3)
. (3)
Сравнив (2) и (3) с (1) получим:
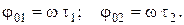
Выполним вычисления:
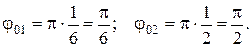
Для определения 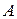 и
и 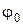 результирующего колебания построим векторную диаграмму (рис.).
результирующего колебания построим векторную диаграмму (рис.).
Для гармонического колебания 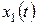 :
: 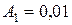 м;
м; 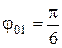 рад.
рад.
Для гармонического колебания 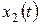 :
: 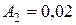 м;
м; 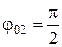 рад.
рад.
Амплитуда результирующего колебания является диагональю параллелограмма, построенного на векторах  и
и 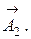
По теореме косинусов
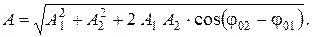
 |
Рис.
Выполним вычисление амплитуды результирующего колебания:
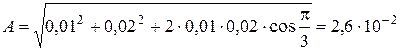 м.
м.
Так как

то
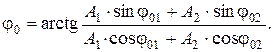
Выполним вычисления начальной фазы результирующего колебания:
 рад.
рад.
Так как частоты складываемых колебаний одинаковы, то результирующее колебание будет иметь ту же частоту, и уравнение этого колебания будет иметь вид:
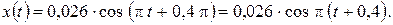
Ответ: 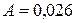 м;
м; 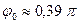 рад;
рад; 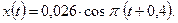
Дата добавления: 2015-02-10; просмотров: 336; Мы поможем в написании вашей работы!; Нарушение авторских прав |