Совместимость по типу

Операции объединения, пересечения и вычитания требуют от операндов совместимости по типу. Будет говорить, что два отношения совместимы по типу, если у них эквивалентные схемы, а точнее:

1. если каждое их них имеет одно и то же множество атрибутов (а значит и одинаковую степень)

2. если возможно такое упорядочение атрибутов в схемах, что на одинаковых местах будут находиться сравнимые атрибуты, т.е. атрибуты, определенные на одном и том же домене

Пример: имеются следующие отношения (Рис. 2-17)

Отношение Продукты1 содержит продукты, имеющиеся в магазине

Отношение Продукты2 содержит продукты, поставляемые поставщиком P2

Отношение Поставщики содержит поставщиков продуктов

Отношение ВидПродукта содержит виды продуктов

Первые три отношения имеют одинаковую степень, т.е. выполняется первое условие совместимости по типу. Второе условие выполняется только для отношений Продукты1 и Продукты2, т.е. только эти отношения совместимы по типу, а значит с ними можно выполнять операции объединения, пересечения и вычитания.

Рис. 2-17. База данных продуктов и поставщиков (значения для примера)

Теоретико-множественные операции реляционной алгебры

Объединением двух совместимых по типу отношений А и В называется отношение с тем же заголовком, как в исходных отношениях, и с телом, состоящим из множества всех кортежей, принадлежащих А или В или обоим отношением (за исключением повторяющихся).

Пусть заданы два отношения A={a}, B={b}, где a и b – соответственно кортежи отношений A и B, то объединение

A!!!!!!!!!!!!!!!!!B = {c | c∈A ∨ c∈B},

Здесь c – кортеж нового отношения, ∨ – операция логического сложения «ИЛИ».

Пример: Объединим, приведенные на Рис. 2-17, отношения Продукты1 (содержащее продукты, имеющиеся в магазине) и Продукты2 (содержащее продукты, поставляемые поставщиком P2). Результатом объединения станет отношение R1 (Рис. 0-18), содержащее продукты, которые или имеются в магазине или поставляются поставщиком P2 (либо и то и другое).

Обратите внимание, что дублирующие кортежи исключены из результирующего отношения R1.

Рис. 2-18. Пример объединения

Пересечением двух совместимых по типу отношений А и В называется отношение с тем же заголовком, как в исходных отношениях, и с телом, состоящим из множества всех кортежей, принадлежащих одновременно обоим отношением А и В.

AЁ!!!!!!!!!!!!!!!!B = {c | c∈A ∧ c∈B}, Здесь ∧ – операция логического умножения (логическое «И»).

Пример: Пересечением отношений Продукты1 и Продукты2 (Рис. 2-17) станет отношение R2 (Рис. 2-19), содержащее продукты, имеющиеся в магазине и поставляемые поставщиком P2.

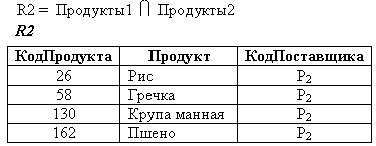
Рис. 2-19. Пример пересечения

Вычитанием двух совместимых по типу отношений А и В называется отношение с тем же заголовком, как в исходных отношениях, и с телом, состоящим из множества всех кортежей, принадлежащих отношению А и не принадлежащих отношению В.

A \ B = {c | c∈A ∧ c∉B}

Отметим, что операции объединения и пересечения являются коммутативными операциями, т.е. результат операции не зависит от порядка аргументов в операции. Операция вычитания является несимметричной операцией, т.е. результат операции будет различным для разного порядка аргументов.

Пример: При вычитании отношения Продукты2 из отношения Продукты1 (Рис. 2-17) получится отношение R3 (Рис. 2-20), содержащее продукты, имеющиеся в магазине, кроме тех продуктов, которые поставляет поставщик P2.

При вычитании отношения Продукты1 из отношения Продукты2 получится другое отношение R4 (поскольку операция вычитания не коммутативная). Отношение R4 (Рис. 2-20) будет содержать продукты, поставляемые поставщиком P2, кроме тех продуктов, которые имеются в магазине.

Рис. 2-21. Примеры вычитания

Расширенное декартово произведение

Эта операция не накладывает никаких дополнительных условий на схемы исходных отношений, поэтому операция расширенного декартова произведения допустима для любых двух отношений.

Прежде чем определить саму операцию, введем дополнительно понятие конкатенации, или сцепления, кортежей.

Сцеплением, или конкатенацией, кортежей c = <c1,c2,…,cn> и q = <q1,q2,…,qm> называется кортеж, полученный добавлением значений второго в конец первого. Сцепление кортежей c и q обозначается как (c,q).

(c,q) = <c1,c2,…,cn,q1,q2,…,qm>

здесь n – число элементов в первом кортеже c, m – число элементов во втором кортеже q.

Все предыдущие операция не меняли степени или арности отношений – это следует из определения эквивалентности схем отношений. Операция расширенного декартова произведения меняет степень результирующего отношения.

Расширенное декартово произведение двух отношений А и В, где А и В не имеют общих атрибутов, определяется как отношение с заголовком, который представляет собой сцепление двух заголовков исходных отношений А и В, и телом, состоящим из множества всех кортежей c, таких, что c представляет собой сцепление кортежа a, принадлежащего отношению A, и кортежа b, принадлежащего отношению B.

Т.е. если A={a}, B={b}, то расширенное декартово произведение A ⊗ B = {(a,b) | a∈A ∧ b∈B}

Обратите внимание, что кардинальное число результата равно произведению кардинальных чисел исходных отношений А и В, а степень равна сумме их степеней. Операция декартова произведения довольно редко используется как самостоятельная операция, чаще результат этой операции подвергается дальнейшей обработке.

Пример: Декартовым произведением отношений Поставщики и ВидПродукта (Рис. 2-17) будет отношение R5 (Рис. 2-21). Отношение R5 соответствует ситуации, когда все поставщики поставляют все виды продуктов.

Рис. 2-21. Пример расширенного декартова произведения

Операцию декартова произведения, с учетом возможности перестановки атрибутов в отношении, можно считать коммутативной. Таким образом, все операции, кроме вычитания, являются коммутативными, т.е.

AB = BA

AB = BA

A ⊗B = B ⊗ A

Все теоретико-множественные операции являются ассоциативными операциями, т.е.

A(BC) = (AB)C = ABC

A(BC) = (AB)C = ABC

A \ (B \ C) = (A \ B) \ C = A \ B \ C

A⊗(B⊗C) = (A⊗B) ⊗C = A⊗B⊗C

Специальные реляционные операции

Выборка (ограничение, горизонтальное подмножество)

Для определения этой операции необходимо ввести дополнительные обозначения.

Пусть α – булевское выражение, составленное из термов сравнения с помощью связок И (∧), ИЛИ (∨), НЕ (-) и, возможно, скобок. В качестве термов сравнения допускаются:

1. терм А θ а,

где А – имя некоторого атрибута, принимающего значения из домена D; а – константа, взятая из того же домена D, а ∈ D; θ – одна из допустимых для данного домена D операций сравнения (=, ≠, <, ≤, >, ≥);

2. терм А θ В,

где А, В – имена некоторых θ-сравнимых атрибутов, то есть атрибутов, принимающих значение из одного и того же домена D.

Тогда выборкой (θ-выборкой), заданной на отношении А в виде булевского выражения, определенного на атрибутах отношения А, называется отношение, имеющее тот же заголовок, что и отношение А, и тело, содержащее множество всех кортежей отношения А, для которых истинно условие выбора или ограничения:

А[α(t)] = {t | t ∈ A ∧ α(t) = “Истина”}

Операция ограничения является одной из основных при работе с реляционной моделью данных. Условие α может быть сколь угодно сложным.

Пример:

• Результатом выборки продуктов, поставляемых поставщиком P3, из отношения Продукты1 (Рис. 2-17) будет отношение R6 (Рис. 2-22, a)

• Результатом выборки Владивостокских поставщиков из отношения Поставщики (Рис. 2-17) будет отношение R7 (Рис. 2-22, b)

Рис. 2-22. Примеры операций выборки

Проекцией отношения A по атрибутам X, Y, …, Z, где каждый из атрибутов принадлежит отношению A(A[X, Y, …, Z]), называется отношение с заголовком {X, Y, …, Z} и телом, содержащим множество всех кортежей {X:x, Y:y, …, Z:z}, таких, для которых в отношении A значение атрибута X равно x, атрибута Y равно y, …, атрибута Z равно z. Таким образом, с помощью оператора проекции получено «вертикальное» подмножество данного отношения, т.е. подмножество, получаемое исключением всех атрибутов, не указанных в списке атрибутов, и последующим исключением дублирующих кортежей (подкортежей) из того, что осталось.

Никакой атрибут не может быть указан в списке атрибутов более одного раза.

Пример:

• Проекцией отношения Продукты1 (Рис. 2-17) по атрибуту КодПоставщика будет отношение R8 (Рис. 2-23, a). Обратите внимание, что дублирующие кортежи исключены из отношения R8

• Проекцией отношения Поставщики (Рис. 2-17) по атрибуту Город будет отношение R9 (Рис. 2-23, b)

• Довольно часто операция проекции используется в сочетании с другими операциями. Например, нужно выбрать названия поставщиков из Владивостока (на основе отношения Поставщики – Рис. 2-17). Сначала выполняется операция выборки, а затем – проекции (Рис. 2-23, c).

Рис. 2-23. Примеры операций проекции

Соединение (естественное, условное)

Операция соединения имеет несколько разновидностей. Однако наиболее важным является естественное соединение, поэтому часто для обозначения именно естественного соединения используют общий термин «соединение».

Пусть отношения A и B имеют заголовки:

{X1, X2,…, Xm, Y1, Y2,…, Yn}

и

{ Y1, Y2,…, Yn, Z1, Z2,…, Zp} соответственно;

т.е. атрибуты Y1, Y2,…, Yn (и только они) – общие для двух отношений;

X1, X2,…, Xm – остальные атрибуты отношения A; Z1, Z2,…, Zp – остальные атрибуты отношения B. Предположим также, что соответствующие атрибуты (т.е. атрибуты с одинаковыми именами) определены на одном и том же домене. Будем рассматривать выражения {X1, X2,…, Xm}, {Y1, Y2,…, Yn}, {Z1, Z2,…, Zp} как три составных атрибута X, Y, Z соответственно.

Тогда естественным соединением отношений A и B называется отношение с заголовком {X, Y, Z}и телом, содержащим множество всех кортежей {X:x, Y:y, Z:z}, таких, для которых в отношении A значение атрибута X равно x, а атрибута Y равно y, и в отношении B значение атрибута Y равно y, а атрибута Z равно z.

Естественное соединение обладает свойствами коммутативности и ассоциативности.

Отметим также, что если отношения A и B не имеют общих атрибутов, то естественное соединение превращается в декартово произведение.

Пример: Рассмотрим отношения Продукты1 и Поставщики (Рис. 2-17). Атрибуты КодПоставщика и КодП определены на одном и том же домене кодов поставщиков. Поскольку при естественном соединении также требуется, чтобы общие атрибуты соединяемых отношений имели одинаковые имена, переименуем атрибут КодП отношения Поставщики в КодПоставщика. Тогда естественным соединением отношений Продукты1 и Поставщики по атрибуту КодПоставщика будет отношение R11 (Рис. 2-24).

Рис. 2-24. Пример естественного соединения

Рассмотрим теперь условное соединение (или θ-соединение). Эта операция используется, когда необходимо соединить два отношения на основе некоторых условий, отличных от эквивалентности.

Пусть отношения A и B не имеют общих имен атрибутов, и θ определяется как в операции выборки. Тогда условным соединением отношения A по атрибуту X с отношением B по атрибуту Y называется отношение с заголовком, который представляет собой сцепление двух заголовков исходных отношений А и В (как и при операции декартова произведения), и с телом, содержащим множество кортежей t, таких что t принадлежит этому декартову произведению и вычисление условия “X θ Y” дает значение «истина» для этого кортежа. Атрибуты X и Y должны быть определены на одном и том же домене, а операция должна иметь смысл для этого домена.

Пример: Получить названия продуктов (отношение Продукты1 – Рис. 2-17), поставляемых поставщиками из Владивостока (отношение Поставщики – Рис. 2-17). По сути, в этом примере необходимо использовать две операции: условного соединения – для получения непосредственно списка продуктов, поставляемых Владивостокскими поставщиками (R12); и проекции – для получения только названий продуктов (R13) (Рис. 2-25).

Рис. 2-25. Пример условного соединения

Деление

Пусть отношения A и B имеют заголовки:

{X1, X2,…, Xm, Y1, Y2,…, Yn}

и

{ Y1, Y2,…, Yn } соответственно;

т.е. атрибуты Y1, Y2,…, Yn – общие для двух отношений, и отношение A имеет дополнительные атрибуты X1, X2,…, Xm, а отношение B не имеет дополнительных атрибутов. (Отношения A и B представляют соответственно делимое и делитель). Предположим также, что соответствующие атрибуты (т.е. атрибуты с одинаковыми именами) определены на одном и том же домене. Пусть выражения {X1, X2,…, Xm}и {Y1, Y2,…, Yn} обозначают два составных атрибута X и Y соответственно.

Тогда делением отношений A и B называется отношение с заголовком {X} и телом, содержащим множество всех кортежей {X:x} таких, что существует кортеж {X:x, Y:y}, который принадлежит отношению A для всех кортежей {Y:y}, принадлежащих отношению B.

Нестрого это можно сформулировать так: результат содержит такие X-значения из отношения A, для которых соответствующие Y-значения (из A) включают все Y-значения из отношения B.

Если запрос на естественном языке включает слово “все” (“получить поставщиков, поставляющих все виды продуктов”), то почти наверняка потребуется операция деления.

Пример: Пусть отношение R14 содержит поставщиков и виды поставляемых ими продуктов, а отношение ВидПродукта содержит виды продуктов (Рис. 2-26). Тогда, чтобы получить поставщиков поставляющих ВСЕ виды продуктов, необходимо отношение R14 разделить на отношение ВидПродукта по атрибуту КодВида (Рис. 2-26).

Рис. 2-26. Пример операции деления

Итак, мы рассмотрели операции реляционной алгебры. Эти восемь операций (объединение, пересечение, вычитание, декартово произведение, выборка, проекция, соединение, деление) не представляют собой минимальный набор операций. Т.е. некоторые операции можно выразить через другие операции, а именно – соединение, пересечение и деление. Например, соединение – это проекция выборки декартова произведения. Таким образом, примитивными операциями, т.е. которые нельзя выразить через другие операции, являются остальные пять операций: объединение, вычитание, выборка, проекция, декартово произведение. Эти пять примитивных операций будут составлять минимальный набор операций реляционной алгебры.

Однако на практике другие три операции (особенно соединение) настолько часто используются, что имеет смысл обеспечить их непосредственную поддержку, несмотря на то, что они не примитивны.

Примеры использования операций реляционной алгебры

Рассмотрим несколько примеров для демонстрации возможностей операций реляционной алгебры.

I. Пусть даны три отношения с эквивалентными схемами: (ФИО, Должность, Отдел). Отношение R1 содержит список сотрудников предприятия, работающих над проектом P1, R2 – список сотрудников, работающих над проектом P2, R3 – список сотрудников, живущих во Владивостоке. Сотрудники могут работать над несколькими проектами.

Составить формулы для следующих запросов:

1. Список сотрудников, живущих не во Владивостоке, т.е. это такие сотрудники, которые могут содержаться в отношении R1 или R2 или обоих отношениях, но не входят в отношение R3 R1R2 \ R3 или (R1 \ R3) (R2 \ R3) этот пример показывает, что один и тот запрос можно сформулировать несколькими способами

2. Список сотрудников, работающих над двумя проектами и живущих во Владивостоке, т.е. это сотрудники, содержащиеся во всех трех отношениях R1R2R3

3. Список сотрудников, работающих только над одним из проектов (R1R2) \ (R1R2)

4. Список сотрудников, работающих только над одним из проектов, и живущих во Владивостоке (R1R2) \ (R1R2) R3 или (R1R3)(R2R3) \ (R1R2)

II. Даны следующие отношения:

R1(Таб№, ФИО, Должность, Отдел) – список сотрудников по отделам

R2(Должность, Оклад) – должностные оклады

R3(Должность, Отдел) – штатные должности по отделам, т.е. какие должности должны быть в каждом отделе.

Сотрудник может занимать несколько должностей в одном и том же или разных отделах. Составить формулы для следующих запросов:

1. Табельные номера и ФИО сотрудников отдела “Бухгалтерия” (R1[Отдел = “Бухгалтерия”]) [Таб№, ФИО]

2. ФИО сотрудников с окладом больше 3000 руб (R1[R1.Должность = R2.Должность ∧ R2.Оклад > 3000]R2) [ФИО]

3. Список вакантных должностей в отделах R3 \ (R1[Должность, Оклад])

4. Отделы, не имеющие по штату должность “Мастер” R3 \ R3[Должность = “Мастер”]

5. ФИО сотрудников, занимающих больше одной должности (R1[R1.ФИО = R1’.ФИО ∧ R1.Должность ≠ R1’.Должность]R1’)[ФИО] Обратите внимание, что для поиска строк, удовлетворяющих условию больше одного, применяется операция соединения отношения с самим собой. Поэтому мы взяли копию отношения R1 и назвали ее R1’.

6. ФИО сотрудников, занимающие только одну должность найдем сначала сотрудников, занимающих больше одной должности R4 = (R1[R1.ФИО = R1’.ФИО ∧ R1.Должность ≠ R1’.Должность]R1’)[ФИО] вычтем из проекции R1 по ФИО полученное отношение R4 (R1[ФИО]) \ R4

7. Отделы, имеющие в штате, по крайней мере, все те должности, что и в отделе “Цех 1” найдем все должности положенные по штату в отделе “Цех1” R4 = (R3[Отдел = “Цех 1”]) [Должность] ответ на поставленный вопрос R3[Должность ÷ Должность]R4

2.2.4. Алгоритм перехода от модели «сущность-связь» к реляционной модели

Модель «сущность-связь» используется на ранних стадиях проектирования БД. Как уже говорилось модель «сущность-связь» является концептуальной моделью и не учитывает особенности конкретной СУБД (допустимые типы и наименования полей и таблиц, ограничения целостностии т.п.). Существует алгоритм однозначного преобразования модели «сущность-связь» в реляционную модель данных (т.е. осуществляется переход от инфологического моделирования к логическому проектированию схемы реляционной БД). Рассмотрим этот алгоритм.

1. Каждой сущности модели «сущность-связь» ставится в соответствие отношение реляционной модели. При этом на имена отношений накладываются ограничения, присущие конкретной СУБД.

2. Каждый атрибут сущности становится атрибутом соответствующего отношения. На имена атрибутов отношения также накладываются ограничения выбранной СУБД. Для каждого атрибута задается конкретный допустимый в СУБД тип данных и обязательность или необязательность данного атрибута (т.е. допустимость или недопустимость Null-значений)

3. Первичный ключ сущности становится первичным ключом соответствующего отношения. Атрибуты, входящие в первичный ключ отношения, автоматически получают свойство отсутствия неопределенных значений (Not Null).

4. В каждое отношение, соответствующее сущности со стороны «многие» (связь 1:N), добавляется набор атрибутов сущности со стороны «один», являющихся первичным ключом сущности со стороны «один». В отношении, соответствующим сущности со стороны «многие», этот набор атрибутов становится внешним ключом.

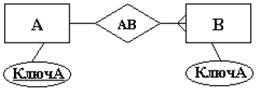
5. Для моделирования необязательного класса принадлежности у атрибутов, соответствующих внешнему ключу, устанавливается свойство допустимости неопределенных значений. При обязательном классе принадлежности атрибуты получают свойство отсутствия неопределенных значений.

6. Разрешение связей типа M:N. Связи становится в соответствие отношение, имеющего атрибуты, которые в сущностях являются первичными ключами, а в новом отношении будут внешними ключами. Первичным ключом нового отношения будет совокупность внешних ключей.

Пример преобразования модели «сущность-связь» к реляционной модели

Рассмотрим на примере, как осуществить переход от модели «сущность-связь» к реляционной модели. Возьмем пример, приведенный в параграфе 2.1.2.На Рис. 2-14 приведен окончательный вариант диаграммы «сущность-связь».

1. В указанной модели мы имеем дело со следующими сущностями: Продукты, Поставщики, Города, Продажи. Следовательно, и в реляционной модели будут участвовать четыре отношения с такими же именами.

2. Далее в процессе задания конкретных типов данных для каждого атрибута отношений (домены могли быть определены уже на этапе инфологического моделирования) получаем отношения, приведенные на Рис. 2-27. Таблица 2-4 содержит типы данных для каждого атрибута.

3. Первичные ключи отношений, описанных в Таблица 2-4, помечены знаком √.

Рис. 2-27. Переход от сущностей ER-модели к отношениям реляционной модели

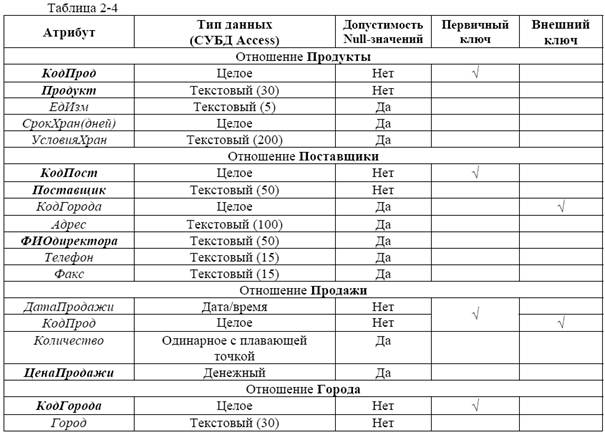
4. Степень связи между сущностями Поставщики и Города – N:1, поэтому первичный ключ КодГорода (сущности Города) должен войти в сущность Поставщики в качестве внешнего ключа (мы это сделали еще на этапе создания модели «сущность-связь»); степень связи между сущностями Продажи и Продукты – N:1, поэтому первичный ключ КодПрод (сущности Продукты) должен войти в сущность Продажи в качестве внешнего ключа (мы это сделали еще на этапе создания модели «сущность-связь»).

5. Для внешнего ключа КодГорода (отношение Поставщики) устанавливаем свойство допустимость Null-значений: «Да», т.к. в модели «сущность-связь» сущность Поставщики имела необязательный класс принадлежности; для внешнего ключа КодПост (отношение Поставщики) устанавливаем свойство допустимость Null-значений: «Нет», поскольку этот внешний ключ входит в состав первичного ключа (Таблица 0-4).

6. В нашем примере две связи имеют степень M:N. Это связи Поставляют и Заказаны. Следовательно, дополнительно появляются еще два отношения Поставки и Заказы соответственно. Таблица 0-5 содержит описание атрибутов этих отношений.

Рис. 2-28. Реляционная модель данных учета продажи продуктов в магазине