Нормирование метрологических характеристик средств измерений.

Типовые метрологические характеристики первой группы нормируют как номинальные характеристики средств изме­рений данного типа. Номинальную функцию преобразования измерительного преобразователя представляют в виде фор­мулы, таблицы, графика. Номинальные значения однозначной или многозначной меры представляют именованными числа­ми.

Для конкретных экземпляров средств измерений норми­руются пределы (граничные характеристики), в которых должна находиться индивидуальная метрологическая ха­рактеристика первой группы при предусмотренных усло­виях применения средства измерений.

Нормальные и рабочие условия применения средств изме­рений устанавливаются в нормативно-технических докумен­тах на средства измерений. Нормальными считаются условия, при которых зависимостью метрологических характеристик от изменения значений влияющих величин можно пренебречь. Так, для многих типов средств измерений нормальными усло­виями являются: температура — (293±5) К, относительная влажность — (65 ± 15) %, напряжение в сети питания — 220 В ± 10 %. Рабочие условия отличаются от нормальных более широким диапазоном изменения значений влияющих величин.

При нормировании метрологических характеристик вто­рой группы исходят из того, что правильность показаний средств измерений обеспечивается поправкой, точное значе­ние которой для каждого конкретного экземпляра средств измерений неизвестно. Поэтому устанавливают пределы, в которых должна находиться поправка у всех средств изме­рений данного типа. Прибегают также к ситуационному моде­лированию и нормируют пределы, в которых должны нахо­диться аналоги числовых характеристик ситуационной моде­ли. Точность показаний нормируется указанием предельно допустимого значения среднего квадратического отклонения (или его оценки). Так как показание и поправка суммируют­ся, то может нормироваться аналог среднего квадратического отклонения композиции закона распределения вероятности показания и ситуационной модели поправки.

Нормированные метрологические характеристики второй группы представляются либо одним числом, либо функцией (формулой, таблицей, графиком) информативного параметра входного или выходного сигнала.

Нормирование метрологических характеристик второй группы может производиться как для нормальных, так и для рабочих условий. В отличие от этого метрологические харак­теристики третьей группы нормируются только для рабочих условий измерений. В рабочих условиях изменение значений влияющих величин начинает сказываться на точности и пра­вильности показаний. Это учитывается функциями влияния. Для разных экземпляров средств измерений данного типа могут различаться как вид этих функций, так и их парамет­ры. Однако в принципе, для всех экземпляров средств изме­рений данного типа эти функции должны быть подобны, а их параметры близки. Поэтому нормируются в качестве номи­нальных некоторые усредненные функции влияния с указа­нием их параметров. Нормируются также пределы допускае­мых отклонений функций влияния у отдельных экземпляров средств измерений данного типа от номинальной. Если функ­ции влияния у различных экземпляров средств измерений данного типа существенно различаются между собой, то нормируются граничные функции влияния.

В нормативно-технических документах номинальная функ­ция влияния, пределы допускаемых отклонений от нее и гра­ничные функции влияния представляются в виде числа, фор­мулы, таблицы или графика. Линейную функцию влияния, проходящую через начало координат, допускается представ­лять коэффициентом влияния в виде числа. Функции влияния представляют в координатах, у которых начало отсчета по оси ординат совпадает с нормальным значением влияющей вели­чины на оси абсцисс.

Пределы допускаемых изменений метрологических ха­рактеристик, вызванных изменениями влияющих величин, устанавливают в виде границ зоны вокруг значения метроло­гической характеристики при нормальных условиях.

Аналогично нормируются метрологические характеристи­ки четвертой группы. Устанавливается номинальная динами­ческая характеристика, пределы допускаемых отклонений от нее и граничные динамические характеристики. Они предс­тавляются в виде числа, формулы, таблицы или графика.

Во всех случаях представление нормированных метроло­гических характеристик в виде графика допускается только при одновременном представлении их в виде формулы или таблицы.

Формы представления нормированных метрологических характеристик пятой и шестой групп устанавливаются в нор­мативно-технических документах на средства измерений конк­ретных видов и типов.

В зависимости от особенностей использования средств из­мерений возникает необходимость в том или ином наборе их метрологических характеристик. Так, для вещественных мер и цифро-аналоговых преобразователей, аналоговых и цифро­вых измерительных показывающих и регистрирующих при­боров, аналоговых и аналого-цифровых измерительных пре­образователей нормируются разные наборы метрологических характеристик. Номенклатура нормированных метрологичес­ких характеристик в каждом наборе зависит кроме того от от­ветственности измерений и других факторов. Подробно все вопросы нормирования метрологических характеристик средств измерений регламентированы ГОСТ 8.009—84.

Использование нормированных метрологических характе­ристик для определения в реальных условиях эксплуатации точности показаний средств измерений и поправки, обеспечи­вающей их правильность, рассмотрим на примере.

Пример 23.В нормативно-технической документации на вольтметр приведены следующие его нормированные метрологические характеристики:

1. В нормальных условиях измерений (при температуре 20° С и напряжении питания 220 В) аддитивная поправка Q_H к показаниям у приборов этого типа находится в пределах от –10мВ до 10мВ; среднее квадратическое отклонение показания s_H не превышает 5мВ,

2. Номинальная функция влияния температуры на поправку

Y_q(t) = ¾ K_q(t)(t-t_H)

номинальная функция влияния напряжения в сети питания на поправку

Y_q(U) = ¾ K_q(U)(U-U_H)

где t_H = 20^oС и U_H = 220 В — нормальные значения влияющих величин, а номинальные значения коэффициентов влияния температуры и напря­жения питания K_q(t) = 0,5 мВ/°С; K_q(U) = 0,4 мВ/В.

Номинальная функция влияния температуры на среднее квадратическое отклонение показания

Y_s(t) = ¾ K_s(t)(t-t_H)

номинальная функция влияния напряжения в сети питания на среднее квадратическое отклонение показания

Y_s(U) = ¾ K_s(U)(U-U_H)

где К_s(t) = 0,1мВ/°С; K_s(u) = 0,1 мВ/В.

Требуется определить поправку, обеспечивающую правильность показания вольтметра в рабочих условиях измерений

25°С £ t £ 35°С;

200 В £ U £230В,

и точность показания.

Решение. 1. Неопределенность аддитивной поправки Q_H в нормаль­ных условиях учитывается ситуационной моделью, показанной на рис. 55, а. Если неопределенность рабочих условий измерений также отразить с помощью ситуационных моделей, то ситуационные модели номинальных функций влияния на поправку температуры и напряжения питания будут выглядеть так, как они показаны на рис. 55, б, в. Число­вые характеристики всех трех ситуационных моделей, показанных на рис.55,

Функции влияния на поправку являются аддитивными добавками к ее значению в нормальных условиях измерений. Поэтому ситуационная модель поправки в рабочих условиях измерений будет композицией ситуационных моделей, показанных на рис. 55. Ее числовые характерис­тики

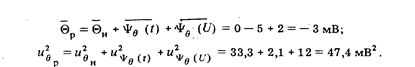
Таким образом, для обеспечения в рабочих условиях измерении правильности показания вольтметра в него нужно вносить поправку - 3 мВ.

2. Точность показания определяется аналогом его среднего квадра-тического отклонения после внесения поправки. Аналог дисперсии показания после внесения поправки

поскольку номинальные функции влияния на среднее квадратическое отклонение показания являются аддитивными добавками к его значе­нию в нормальных условиях. Для простоты возьмем максимальные значения номинальных функций влияния

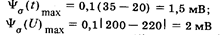
и среднего квадратического отклонения показания в нормальных ус­ловиях, что будет соответствовать наихудшему случаю. Тогда

u² _P = 47,4 + (5 + 1,5 + 2) ² = 119,65 мВ².

Таким образом, в рабочих условиях измерений точность показания вольтметра характеризуется аналогом среднего квадратического откло­нения