Обобщенный закон Гука. Удельная потенциальная энергия упругой деформации при сложном напряженном состоянии

Ранее была получена зависимость, выражающая закон Гука для линейного напряженного состояния (глава 3 “Растяжение-сжатие”).

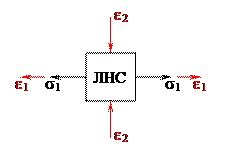
Получим аналогичные зависимости для плоского или объемного напряженных состояний, которые называются сложным напряженным состоянием.

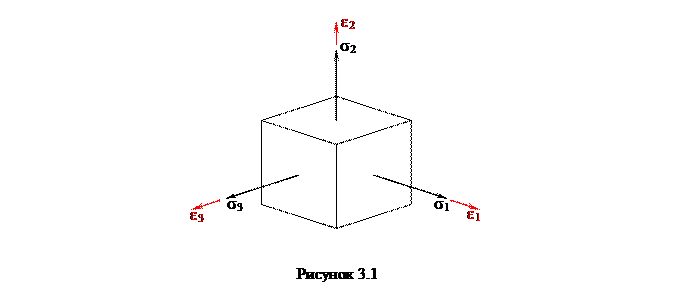
Найдем главную деформацию по направлению e₁ (рисунок 3.1) как сумму деформаций от напряжений s₁, s₂, s₃, которые являются, соответственно, одно продольной и двумя поперечными:

Подставим (3.1) в (3.2), получим:

Аналогично получаем две другие главные деформации e₂ и e₃, тогда зависимости обобщенного закона Гука имеют вид:

(3.3)*

Удельная потенциальная энергия упругой деформации.

Раньше (см. главу 3 “Растяжение-сжатие”) для случая линейного напряженного состояния была получена зависимость для удельной потенциальной энергии упругой деформации следующего вида:

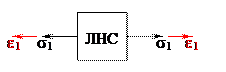
Получим аналогичную зависимость для удельной потенциальной энергии упругой деформации в случае плоского или объемного напряженный состояний. Для этого составим сумму произведений главных напряжений на соответствующие главные деформации аналогично (3.4):

С учетом (3.3) преобразуем (3.5), получим уравнение удельной потенциальной энергии упругой деформации для сложного напряженного состояния.

Потенциальная энергия упругой деформации затрачивается как на изменение формы, так и на изменение объема деформируемого тела, т. е.

где u_Ф, u_V – удельная потенциальная энергия формоизменения и изменения обьема, соответственно, определяются по формулам

Используя зависимости удельной потенциальной энергии упругой деформации и её составляющих, можно разработать способы оценки прочности элементов конструкций и деталей машин. В курсе сопротивления материалов в качестве такого способа широко применяются так называемые гипотезы прочности (или теории пластичности и разрушения).

§4 Теории прочности (гипотезы)

В случае линейного напряженного состояния оценка прочности выполняется по следующей схеме

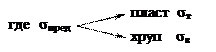Для сложного напряженного состояния эта схема неприменима, т. к. сложно установить расчетный критерий разрушающего напряжения и с другой стороны весьма трудоемко экспериментально определить предельное напряжение материала. Для решения этой задачи предлагается заменить сложное напряженное состояние линейным или одноосным, но эквивалентным по прочности заданному, т.е.

Тогда для эквивалентного н.с. оценку прочности выполняют по следующему условию

где [σ] – допускаемое напряжение, принимается как для обычного линейного напряженного состояния см. условие (3.10).

Величину эквивалентного напряжения определяют с помощью различных гипотез (разрушения и пластичности), в которых за критерий разрушения или пластичности принимаются разнообразные параметры напряженно деформированного состояния конструкции. Рассмотрим некоторые из этих гипотез (теорий).

I теория прочности – теория (критерий или гипотеза) максимальных нормальных напряжений s_max (Галилей / Рэнкин). Эта теория предполагает, что в конструкции происходит разрушение , если одно из наибольших по модулю главных напряжений достигает предельного значения, то условие прочности по этой теории можно представить в таком виде

*

где [σ_р]; [σ_с] – допускаемое напряжение материала конструкции, соответственно, на растяжение или сжатие.

Эта теория применяется для очень хрупких материалов (например, фарфор, стекло, керамика и т.п.).

II теория прочности – теория максимальных относительных деформаций ε_max (Мариотт / Сен-Венан). Используя зависимость обобщенного закона Гука можно записать, что

.

В этом случае условие прочности имеет вид

Теория применяется только для хрупких материалов (чугун, бетон, кирпич и пр.).

III теория прочности – теория максимальных касательных напряжений t_max (Кулон / Треска, Гест).

Условие прочности имеет вид

Теория применяется только для пластичных материалов (сталь, титан, алюминевые сплавы и пр.).

IV теория прочности – критерий максимальных потенциальных энергий изменения формы u_Фmax (энергетическая) (Мизес, Губер, Генки).

Условие прочности имеет вид

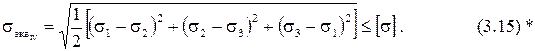
Теория также применима для пластичных материалов.

V теория прочности – эмпирическая теория ( О.Мор).

Теория основана на экспериментальных (эмпирических) данных и сводится к следующему (по упрощенной схеме): для данного материала производятся лабораторные испытания на растяжение и сжатие, определяются показатели прочности и строятся два круга напряжений. К полученным кругам проводятся две касательные, которые ограничивают область обеспечения прочности. Для оценки прочности заданного напряженного состояния по двум главным напряжениям строятся круг напряжений, и выясняют его расположение в области обеспечения прочности. Если этот круг не выходит за пределы этой области, то прочность данного напряженного состояния обеспечена, если, выходит – нарушена (рисунок 4.2).

Для V теории прочности условие прочности можно записать в следующем виде

где m – безразмерный коэффициент, определяется следующим образом

V теория прочности применима как для пластичного, так и для хрупкого материалов.

Рассмотренные теории взаимосвязаны между собой, т.е. дают сопоставимые результаты при использовании для соответствующих материалов.