
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
| Основные понятия и формулы | ||
| Алгоритм проверки статистических гипотез | ||
1. По выборочным данным формулируют основную Н0 и альтернативную Н1 гипотезы.
2. Задают уровень значимости α (0,05 или 0,01).
3. В зависимости от Н0 определяют статистический критерий K, имеющий известное распределение.
4. По выборке и формуле критерия K рассчитывают наблюдаемое значение критерия Kнабл.
5. В зависимости от вида Н1 определяют вид критической области W и критические точки по таблице Приложения для распределения критерия K.
6. По результатам проверки: Kнабл  W ? - делают вывод о принятии или отклонении гипотезы Н0.
7. Формулируют общий вывод исходя из поставленной задачи. W ? - делают вывод о принятии или отклонении гипотезы Н0.
7. Формулируют общий вывод исходя из поставленной задачи.
| 

| |
| Проверка гипотез о равенстве числовому параметру | ||
| · дисперсии · математического ожидания · вероятности | 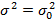
 р = р0
р = р0
| |
| Проверка гипотез о равенстве числовых характеристик | ||
| · дисперсий · математических ожиданий · вероятностей | D(Х) = D(Y) М(Х) = М(Y) рx = рy | |
| Проверка гипотез о законе распределения | ||
| · критерий согласия Пирсона · критерий согласия Колмогорова | 

| |
| Проверка гипотез об однородности выборок | ||
| · критерий Колмогорова-Смирнова · критерий Вилкоксона |  ранговый
ранговый
| |
| Основные умения и навыки: · формулировать статистические гипотезы · оценивать вероятности ошибок принятия гипотезы · проверять статистические гипотезы согласно алгоритму · делать выводы по результатам статистической проверки · использовать возможности Exel для проверки гипотез | ||
Основные этапы проверки
Под статистической гипотезой понимают всякое высказывание о генеральной совокупности (случайной величине), проверяемое по выборке (по результатам наблюдений). Как правило, статистическая гипотеза – это предположение о значении параметров закона распределения (параметрическая) или его виде (непараметрическая).
Не располагая сведениями о всей генеральной совокупности, высказанную гипотезу сопоставляют, по определенным правилам, с выборочными данными и делают вывод о том, можно принять гипотезу или нет. Процедура сопоставления высказанной гипотезы с выборкой называется проверкой гипотезы. Рассмотрим этапы проверки гипотезы и используемые при этом понятия.
Этап 1. Проверяемую гипотезу обычно называют нулевой (или основной) и обозначают Н0. Наряду с нулевой гипотезой рассматривают альтернативную (или конкурирующую) гипотезу Н1, являющуюся логическим отрицанием Н0. Нулевая и альтернативная гипотезы представляют собой две возможности выбора, осуществляемого в задачах проверки статистических гипотез. По выборке будет принято решение о справедливости для генеральной совокупности либо гипотезы Н0, либо гипотезы Н1.
Этап 2. Задаются вероятностью α, которую называют уровнем значимости. Введем ее смысловое значение. Решение о том, можно ли считать высказывание Н0 справедливым для генеральной совокупности, принимается по выборочным данным (т.е. по ограниченному ряду наблюдений), следовательно, это решение может быть как правильным, так и ошибочным.
При проверке любой статистической гипотезы возможны варианты:
· гипотеза Н0 верна и ее принимают (правильное решение);
· гипотеза Н0 не верна и ее отвергают, принимая гипотезу Н1 (правильное решение);
· гипотеза Н0 верна, но ее отвергают согласно правилу проверки (неправильное решение) - это ошибка первого рода;
· гипотеза Н0 не верна, но ее принимают согласно правилу проверки (неправильное решение) – это ошибка второго рода.
Уровень значимости α – это вероятность ошибки первого рода, т.е. вероятность того, что будет принята гипотеза Н1, если на самом деле для генеральной совокупности верна гипотеза Н0. Вероятность α задается заранее малым числом, поскольку это вероятность ошибочного заключения, при этом обычно используют некоторые стандартные значения: 0,05; 0,01; 0,005; 0,001.
Вероятность ошибки второго рода обозначают β – это вероятность того, что будет принята гипотеза Н0, если на самом деле верна гипотеза Н1. Вероятность не совершить ошибку второго рода (1 – β), т. е. вероятность правильного отклонения неверной нулевой гипотезы, называют мощностью критерия.
| Ошибки взаимосвязаны: с уменьшением ошибки α первого рода возрастает вероятность ошибки β второго рода и наоборот. | 
|
| Рис. 1. Взаимосвязь ошибок первого и второго рода. |
Этап 3. Определяют величину специально составленной выборочной характеристики – статистического критерия. В общем случае статистическим критерием называют однозначно определенное правило, устанавливающее условия, при которых проверяемую гипотезу Н0 следует либо отвергнуть, либо принять. Основу критерия составляет специально составленная выборочная характеристика K = f(x1, …, xn) точное или приближенное распределение которой известно.
Этап 4. В формулу критерия K = f(x1, …, xn) вместо (x1, …, xn) подставляют конкретные числа, полученные в результате наблюдений, и подсчитывают числовое значение критерия. Значение критерия, вычисленное по выборке, называют наблюдаемым значением Kнабл.
Этап 5. Далее рассуждают так. Так как. значения критерия позволяют судить о расхождении выборки с нулевой гипотезой, то из области допустимых значений критерия K следует выделить подобласть W таких значений, которые свидетельствовали бы о существенном расхождении данных с гипотезой Н0. Подобласть W называют критической областью.
Критическая область выбирается так, чтобы вероятность попадания в нее была минимальной (равной α), если верна нулевая гипотеза Н0, и максимальной в противоположном случае.
В зависимости от вида конкурирующей гипотезы и распределения критерия выбирают вид расположения критической области: правосторонняя, левосторонняя или двусторонняя. Границы (критические точки) при заданном уровне значимости находят из соотношений для критических областей:
· правосторонней: P(K > Kкр) = α;
· левосторонней: P(K < Kкр) = α;
· двусторонней: P(K < Kкр) = α /2 и P(K > Kкр) = α /2.
Этап 6. Проводят проверку: принадлежит ли наблюдаемое значение критерия критической области.
| Если Kнабл попадает в критическую область W, то гипотеза Н0 отвергается и принимается гипотеза Н1 (на рис. 2 двусторонняя критическая область W показана желтым цветом). Если Kнабл не попадает в критическую область, гипотеза Н0 не отвергается (принимается). | 
|
| Рис. 2. Основной принцип проверки статистических гипотез |
Если гипотеза Н0 принимается, это вовсе не означает, что Н0 является единственно подходящей гипотезой: просто расхождение между выборочными данными и нулевой гипотезой невелико, т. е. Н0 не противоречит результатам наблюдений.
Этап 7. Формулируют общий вывод исходя из поставленной задачи.
Таблица 1. Критические области и критические точки распределений
| Распределение | Критические области и критические точки | ||||
| левосторонняя | двусторонняя | правосторонняя | |||
| z или u Стандартное нормальное | 
| икр = - иправ. кр | Ф(uкр) = (1–α)/2 | Ф(uкр) = (1–2α)/2 | |
| Приложение 2 | |||||
| t Стьюдента | 
| tкр = - tправ. кр | tдв. кр (α; k) | tкр (α; k) | |
| k = n – 1, Приложение 6 | |||||
 Пирсона
Пирсона
| 
|
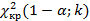
|  ; ;

|
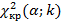
| |
| k = n – 1, Приложение 5 | |||||
| F Фишера | 
| 
| Fправ. кр (α/2; k1; k2);

| Fкр (α; k1; k2) | |
| k1 = nx – 1, k2 = ny – 1, Приложение 7 | |||||
Дата добавления: 2015-04-11; просмотров: 602; Мы поможем в написании вашей работы!; Нарушение авторских прав |