Проверка гипотез о равенстве числовых характеристик генеральных совокупностей

Равенство дисперсий. Пусть имеются две случайные величины, имеющие нормальный закон распределения, причем числовые значения параметров неизвестны. В этом случае проводят выборочные наблюдения и по их данным вычисляют выборочные исправленные дисперсии, оценивающие неизвестные дисперсии. После определения исправленных дисперсий две случайные величины именуют: случайную величину с большей исправленной дисперсией называют Х, а с меньшей – Y.

В основу проверки данной гипотезы положен критерий, который при выполнении нулевой гипотезы имеет распределение Фишера (F-распределение) с числом степеней свободы k_x = n_x – 1 и k_y = n_y - 1. Границы критической области определяют по соответствующему Приложению 7 (таблица Фишера или расширенная таблица Фишера-Снедекора).

В Exel в Пакете анализа присутствует Двухвыборочный F-тест для дисперсии. Здесь проверка всегда односторонняя. Если в графе P(F<=f) односторонняя указана величина, меньшая выбранного Альфа, то основная гипотеза Н₀ отклоняется на уровне значимости α.

Пример 5. Рабочий в начале смены настроил два станка-автомата. Предварительным анализом было установлено, что размер диаметра валиков, изготовленных каждым автоматом, имеет нормальный закон распределения. В конце смены был проведен выборочный контроль 14 деталей, обработанных на первом станке, и 9 деталей - на втором станке и исправленные дисперсии соответственно составили 5мм² и 7 мм². Проверить гипотезу о том, что два станка-автомата имеют одинаковую точность.

Предварительно именуем выборки: с большей дисперсией – X, с меньшей – Y: 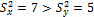, следовательно, и .

1. Принимаем и .

2. Назначаем .

3. Критерий 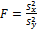, имеющий распределение Фишера ( - распределение) с числом степеней свободы и .

4. .

5. Согласно гипотезе критическая область W – правосторонняя:

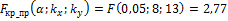(по Приложению 7).

6. Т.к. 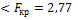нулевая гипотеза принимается при уровне значимости 0,05.

7. Вывод: Станки-автоматы имеют одинаковую точность.

Равенство математических ожиданий (дисперсии известны). Пусть Х и Y – случайные величины, имеющие нормальный закон распределения , , причем числовые значения математического ожидания неизвестны, а числовые значения дисперсии известны. В этом случае проводят выборочные наблюдения и по их данным вычисляют выборочное среднее арифметическое (соответственно и ), которое дает приближенное представление о числовом значении математического ожидания.

В качестве критерия проверки используют величину, которая зависит от выборочных данных и по значению которой можно судить о близости выборочных средних арифметических двух распределений: 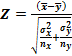. Выбранный критерий при выполнении нулевой гипотезы подчиняется стандартному нормальному закону распределения Z .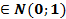

Пример 6. Рабочий в начале смены настроил два станка-автомата: X и Y. Предварительным анализом было установлено, что размер диаметра валиков, изготовленных каждым автоматом, имеет нормальный закон распределения с дисперсией 5 для станка X и 7 для станка Y. В конце смены был проведен выборочный контроль 14 деталей, обработанных на станке X, и 9 деталей - на станке Y. Средние диаметры валиков соответственно составили: для автомата X – 182 мм, для Y – 185 мм. Проверить гипотезу о том, что два станка-автомата настроены на один размер.

1. Принимаем и .

2. Назначаем .

3. Критерий: ,

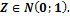
4.

5. Согласно гипотезе критическая область W – левосторонняя:

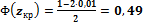и по Приложению 2 и .

6. Т.к. нулевая гипотеза отвергается при уровне значимости 0,01.

7. Вывод: различие выборочных средних неслучайно и станки не настроены на один размер.

Равенство математических ожиданий (дисперсии неизвестны). Пусть Х и Y – случайные величины, имеющие нормальный закон распределения , , причем числовые значения математического ожидания и дисперсии неизвестны. В этом случае проводят выборочные наблюдения и по их данным вычисляют выборочное среднее арифметическое (соответственно и ), которое дает приближенное представление о числовом значении математического ожидания, а также выборочную исправленную дисперсию, оценивающую неизвестную дисперсию ( ).

Применяемый в данном случае критерий Стьюдента предполагает равенство неизвестных дисперсий. Поэтому на предварительном этапе необходимо убедиться в этом предположении. В основу проверки данной гипотезы положен критерий:

который при выполнении нулевой гипотезы имеет распределение Стьюдента с числом степеней свободы k = n_x + n_y – 2.

Пример 7. Рабочий в начале смены настроил два станка-автомата. Предварительным анализом было установлено, что размер диаметра валиков, изготовленных каждым автоматом, имеет нормальный закон распределения. В конце смены был проведен выборочный контроль 14 деталей, обработанных на первом станке, и 9 деталей - на втором станке. Средние диаметры валиков составили: для первого автомата – 182 мм, для второго – 185 мм, а выборочные исправленные дисперсии соответственно 5 и 7 . Проверить гипотезу о том, что два станка-автомата настроены на один размер.

На предварительном этапе именуем выборки: с большей дисперсией – X, с меньшей – Y: , следовательно, и .

1. Принимаем и .

2. Назначаем .

Дополнительно проверяем условие равенства дисперсий - .

3. Критерий: 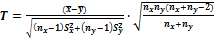, имеющий распределение Стьюдента с числом степеней свободы .

4. .

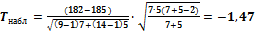5. Согласно гипотезе критическая область W – левосторонняя:

по Приложению 6 находим одностороннюю критическую точку ; .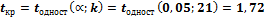

6. Т.к. нулевая гипотеза не противоречит опытным данным и принимается при уровне значимости 0,05.

7. Вывод: Различие выборочных средних случайно и станки настроены на один размер.

Exel позволяет провести испытание гипотезы о равенстве математических ожиданий двух нормальных распределений с случае равенства неизвестных генеральных дисперсий: Анализ данных и Двухвыборочный t-тест с одинаковыми дисперсиями. В графах P(T<=t) дано значение уровня значимости для односторонней и двусторонней проверок. Если это значение меньше заданного Альфа, то основная гипотеза отвергается. Если условие равенства неизвестных генеральных дисперсий не выполняется, следует выбирать Двухвыборочный t-тест с различными дисперсиями.

Таблица 2. Проверка гипотез о равенстве числовому параметру

Гипотеза	Н0	Критерий	Примечание
Равенство дисперсий	D(Х) = D(Y)		-
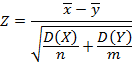
Равенство математических ожиданий	М(Х) = М(Y)		Дисперсии (генеральные) известны
	Дисперсии (генеральные) неизвестны, но равны (предварительно проверить Н0 : D(X)=D(Y))
	Дисперсии (генеральные) неизвестны и неравны
Равенство вероятностей	рx = рy

Равенство вероятностей. На практике часто встречается задача сравнения долей признака (вероятностей) в двух совокупностях. Например, если выборочная доля признака в одной совокупности отличается от такой же доли в другой совокупности, то можно ли считать, что наличие признака в одной совокупности действительно вероятнее, или полученное расхождение является случайным? Для проверки гипотезы из двух генеральных совокупностей составляют выборки достаточно большого объема (n > 30) и по ним определяют выборочные доли (частости), которые являются точечными оценками неизвестных генеральных долей: и . В качестве критерия проверки используют величину, которая зависит от выборочных данных и по значению которой можно судить о близости выборочных долей двух распределений:

. Выбранный критерий при выполнении нулевой гипотезы подчиняется стандартному нормальному закону распределения Z 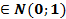. Выборочная доля объединенной выборки определяется по формуле: .

Пример 8. В результате выборочной проверки качества однотипных изделий оказалось, что из 300 изделий фирмы А бракованных – 30, а из 400 фирмы В – 52 изделия. Можно ли считать, что различия в качестве изделий различных фирм существенны?

1. Принимаем и .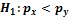

2. Назначаем .

3. Критерий: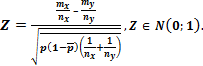

4. и .

5. Согласно гипотезе критическая область W – левосторонняя:

и по Приложению 2 ; .

6. Т.к. нулевая гипотеза не противоречит опытным данным и принимается при уровне значимости 0,05.

7. Вывод: различия в качестве изделий фирм А и В несущественны (случайны).