
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка гипотез о равенстве числовому параметру
Равенство дисперсии числовому параметру. Пусть Х – случайная величина, имеющая нормальный закон распределения  , причем числовое значение дисперсии неизвестно. Дать точный ответ на вопрос, каково числовое значение неизвестного параметра, можно обследовав всю генеральную совокупность, что сделать, как правило, нельзя.
, причем числовое значение дисперсии неизвестно. Дать точный ответ на вопрос, каково числовое значение неизвестного параметра, можно обследовав всю генеральную совокупность, что сделать, как правило, нельзя.
В этом случае проводят выборочные наблюдения и по их данным вычисляют выборочную исправленную дисперсию, которая дает приближенное представление о числовом значении дисперсии. В качестве критерия проверки используют величину, которая зависит от выборочных данных и по значению которой можно судить о близости исправленной дисперсии к предполагаемому значению  . Критерий при выполнении нулевой гипотезыподчиняется распределению Пирсона (
. Критерий при выполнении нулевой гипотезыподчиняется распределению Пирсона (  -распределение) с числом степеней свободыk = n – 1. Границы критической области для n < 30 определяют по Приложению 5, а для n > 30 – по Приложению 2.
-распределение) с числом степеней свободыk = n – 1. Границы критической области для n < 30 определяют по Приложению 5, а для n > 30 – по Приложению 2.
Пример 1. Точность работы станка-автомата проверяется по дисперсии контролируемого размера изделий, которая не должна превышать 0,15 мкм. Выборочному контролю было подвергнуто 25 изделий и по результатам определена исправленная дисперсия 0,25 мкм2. Предполагается, что размер изделия – нормально распределенная случайная величина. Проверить гипотезу, что станок обеспечивает требуемую точность.
1. Принимаем Н0:  и Н1:
и Н1:  .
.
2. Назначаем 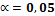 .
.
3. Критерий:  , имеющий распределение Пирсона с числом степеней свободы k=n –1=25–1=24.
, имеющий распределение Пирсона с числом степеней свободы k=n –1=25–1=24.
4.  .
.
5. Согласно гипотезе  критическая область W – правосторонняя:
критическая область W – правосторонняя:
 (по Приложению 5).
(по Приложению 5).
6. Т.к.  нулевая гипотеза отвергается при уровне значимости 0,05.
нулевая гипотеза отвергается при уровне значимости 0,05.
7. Вывод: Станок не обеспечивает требуемой точности.
Равенство математического ожидания числовому параметру (дисперсия известна). Пусть Х – случайная величина, имеющая нормальный закон распределения 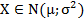 , причем числовое значение математического ожидания
, причем числовое значение математического ожидания  неизвестно, а числовое значение дисперсии
неизвестно, а числовое значение дисперсии  известно (из теоретических соображений или специального исследования при большом числе измерений).
известно (из теоретических соображений или специального исследования при большом числе измерений).
Дать точный ответ на вопрос, каково числовое значение неизвестного параметра, можно обследовав всю генеральную совокупность, что сделать, как правило, нельзя. В этом случае проводят выборочные наблюдения и по их данным вычисляют выборочное среднее арифметическое, которое дает приближенное представление о числовом значении математического ожидания. Далее действуем согласно этапам проверки статистических гипотез.
Пример 2. Темп роста производительности в отрасли прогнозировался на уровне 2,8%. По результатам анализа производительности 10 машиностроительных предприятий было установлено, что средний темп роста составил  . Предполагается, что темп роста есть случайная величина, распределенная по нормальному закону с
. Предполагается, что темп роста есть случайная величина, распределенная по нормальному закону с  Проверить гипотезу, что темп роста производительности в отрасли вышел на прогнозируемый уровень.
Проверить гипотезу, что темп роста производительности в отрасли вышел на прогнозируемый уровень.
1. Принимаем  и
и  .
.
2. Назначаем  .
.
3. Критерий: 
4. 
5. Согласно гипотезе  критическая область W – двусторонняя:
критическая область W – двусторонняя:
a. 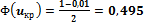 и по Приложению 2
и по Приложению 2  ;
;
b.  и
и  .
.
6. Т.к. 
 нулевая гипотеза отвергается при уровне значимости 0,05.
нулевая гипотеза отвергается при уровне значимости 0,05.
7. Вывод: Темп роста производительности в отрасли не вышел на прогнозируемый уровень 2,8%.
Равенство математического ожидания числовому параметру (дисперсия неизвестна). Это другой случай. Пусть Х – случайная величина, имеющая нормальный закон распределения  , причем числовое значение, как математического ожидания
, причем числовое значение, как математического ожидания  , так и дисперсии
, так и дисперсии  неизвестно. В этом случае по данным наблюдений вычисляют среднее арифметическое и исправленную дисперсию
неизвестно. В этом случае по данным наблюдений вычисляют среднее арифметическое и исправленную дисперсию  . Полученные оценки дают приближенное представление о неизвестных параметрах нормального распределения (соответственно
. Полученные оценки дают приближенное представление о неизвестных параметрах нормального распределения (соответственно  и
и  ) и помогают сформулировать гипотезы.
) и помогают сформулировать гипотезы.
В этом случае по выборке находят только оценку неизвестной дисперсии, а сама генеральная дисперсия НЕ ИЗВЕСТНА. Поэтому в качестве критерия используется Т-критерий, имеющий распределение Стьюдента и ориентированный на малые выборки.
Пример 3. Темп роста производительности в отрасли прогнозировался на уровне 2,6%. Предполагается, что темп роста есть случайная величина, распределенная по нормальному закону. По результатам анализа производительности 10 машиностроительных предприятий было установлено, что средний темп роста составил  , а исправленное среднее квадратическое отклонение – 0,4%. Проверить гипотезу, что темп роста производительности в отрасли вышел на прогнозируемый уровень.
, а исправленное среднее квадратическое отклонение – 0,4%. Проверить гипотезу, что темп роста производительности в отрасли вышел на прогнозируемый уровень.
1. Принимаем  и
и  .
.
2. Назначаем  .
.
3. Критерий:  имеющий распределение Стьюдента (t - распределение) с числом степеней свободы k = n – 1 = 10 – 1 = 9.
имеющий распределение Стьюдента (t - распределение) с числом степеней свободы k = n – 1 = 10 – 1 = 9. 
4.  .
.
5. Согласно гипотезе  критическая область W – левосторонняя:
критическая область W – левосторонняя:
по Приложению 6 находим одностороннюю критическую точку
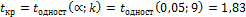 ;
;  .
.
6. Т.к.  нулевая гипотеза не противоречит опытным данным и принимается при уровне значимости 0,05.
нулевая гипотеза не противоречит опытным данным и принимается при уровне значимости 0,05.
7. Вывод: темп роста производительности в отрасли вышел на прогнозируемый уровень 2,6%.
Равенство вероятности числовому параметру. Пусть А – случайное событие, вероятность р появления которого в единичном испытании неизвестна. Выдвинем гипотезу о равенстве р числовому параметру р0. В основе проверки этой гипотезы лежит сравнение числа р0 с приближенным значением вероятности, найденным по экспериментальным данным. Таким приближенным значением является статистическая вероятность или частость события: w = m / n. Далее действуем согласно этапам проверки статистических гипотез.
Пример 4. Партия изделий принимается, если вероятность того, что изделие окажется бракованным, не превышает 2%. Среди случайно отобранных 1000 изделий оказалось 40 бракованных. Можно ли при уровне значимости 0,01 принять партию изделий?
1. Принимаем  и
и  .
.
2. Назначаем  .
.
3. Критерий: 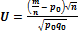

4. 
5. Согласно гипотезе 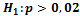 критическая область W – правосторонняя:
критическая область W – правосторонняя:
 и по Приложению 2
и по Приложению 2  ;
;
6. Т.к. 
 нулевая гипотеза отвергается при уровне значимости 0,05.
нулевая гипотеза отвергается при уровне значимости 0,05.
7. Вывод: Партию изделий принять нельзя.
Таблица 2. Проверка гипотез о равенстве числовому параметру
| Гипотеза | Н0 | Критерий | Примечание |
Равенство дисперсии
числовому параметру

|
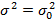
|
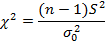
| при k > 30 
|
Равенство математического ожидания числовому параметру

|

| 
| Дисперсия (генеральная) известна |

| Дисперсия (генеральная) неизвестна | ||
| Равенство вероятности числовому параметру | р = р0 | 
| - |
Дата добавления: 2015-04-11; просмотров: 1743; Мы поможем в написании вашей работы!; Нарушение авторских прав |