Эквивалентные формулировки

Гипотеза Римана

Гипотеза Римана утверждает, что:

Все нетривиальные нули дзета-функции имеют действительную часть, равную .

Обобщённая гипотеза Римана

Обобщённая гипотеза Римана (англ. Generalized Riemann hypothesis) состоит из того же самого утверждения для обобщений дзета-функций, называемых L-функциями Дирихле.

Эквивалентные формулировки

В 1901 году Хельге фон Кох показал, что гипотеза Римана эквивалентна следующему утверждению о распределении простых чисел:

при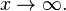

Ещё несколько эквививалентных формулировок:

· Для всех выполняется неравенство

· Для всех выполняется неравенство где ψ(x) — вторая функция Чебышёва,

· Для всех выполняется неравенство где — функция делителей числа , а — постоянная Эйлера-Маскерони.^[3]

· Для всех выполняется неравенство где 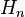— -е гармоническое число.^[4]

· Для любого положительного выполняется неравенство , где — функция Мертенса, см. также обозначение O большое. Более сильная гипотеза была опровергнута в 1985 году^[5].

· Гипотеза Римана эквивалентна следующему равенству: .

· Показано, что гипотеза Римана истинна тогда и только тогда, когда интегральное уравнение

не имеет нетривиальных решений для .

· Если гипотеза Римана неверна, то существует алгоритм, который рано или поздно обнаружит её нарушение. Отсюда следует, что если отрицание гипотезы Римана недоказуемо в арифметике Пеано, то гипотеза Римана верна.