Соображения об истинности гипотезы

В обзорных работах (Bombieri 2000, Conrey 2003, Sarnak 2008) отмечается, что данные в пользу истинности гипотезы Римана сильны, но оставляют место для обоснованных сомнений. Отдельные авторы, однако, убеждены в ложности гипотезы (в частности, так считал Джон Литлвуд).

Среди данных, позволяющих предполагать истинность гипотезы, можно выделить успешное доказательство сходных гипотез (в частности, гипотезы Римана о многообразиях над конечными полями^[9]). Это наиболее сильный теоретический довод, позволяющий предположить, что условие Римана выполняется для всех дзета-функций, связанных с автоморфными отображениями (англ.)русск., что включает классическую гипотезу Римана. Истинность аналогичной гипотезы уже доказана^[10] для дзета-функции Сельберга (англ.)русск., в некоторых отношениях сходной с функцией Римана, и для дзета-функции Госса (англ.)русск. (аналог дзета-функции Римана для функциональных полей).

С другой стороны, некоторые из дзета-функций Эпштейна не удовлетворяют условию Римана, хотя они имеют бесконечное число нулей на критической линии. Однако эти функции не выражаются через ряды Эйлера и не связаны напрямую с автоморфными отображениями.

К «практическим» доводам в пользу истинности Римановской гипотезы относится вычислительная проверка большого числа нетривиальных нулей дзета-функции в рамках проекта ZetaGrid.

Связанные проблемы[править | править вики-текст]

Две гипотезы Харди-Литтлвуда[править | править вики-текст]

В 1914 году Годфри Харольд Харди доказал,^[11] что функция 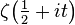имеет бесконечно много вещественных нулей.

Пусть есть количество вещественных нулей, а количество нулей нечётного порядка функции 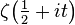, лежащих на интервале .

Две гипотезы Харди и Литлвуда^[12] (о расстоянии между вещественными нулями 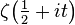и о плотности нулей 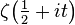на интервалах 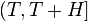при достаточно большом , 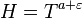и как можно меньшем значении , где 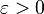сколь угодно малое число), определили два направления в исследовании дзета-функции Римана:

1. Для любого 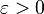существует 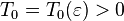, такое что пр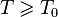и и интервал 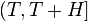содержит нуль нечётного порядка функции .

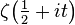2. Для любого 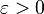существуют такие 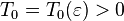и 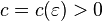, что пр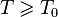и и 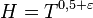справедливо неравенство .