Гипотеза А. Сельберга

В 1942 году Атле Сельберг исследовал проблему Харди-Литтлвуда 2 и доказал, что для любого 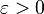существуют 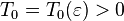и 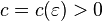, такие что для 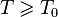и 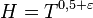справедливо неравенство .

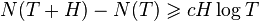В свою очередь, Атле Сельберг высказал гипотезу,^[13] что можно уменьшить показатель степени 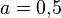для величины .

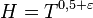В 1984 году А. А. Карацуба доказал^[14][15][16], что при фиксированном с условием , достаточно большом 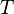и 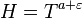, 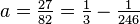промежуток 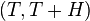содержит не менее 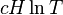вещественных нулей дзета-функции Римана 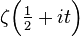. Тем самым он подтвердил гипотезу Сельберга.

Оценки А. Сельберга и А. А. Карацубы являются неулучшаемыми по порядку роста при .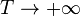

В 1992 году А. А. Карацуба доказал,^[17] что аналог гипотезы Сельберга справедлив для «почти всех» промежутков 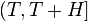, , 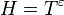где — сколь угодно малое фиксированное положительное число. Метод, разработанный Карацубой, позволяет исследовать нули дзета-функции Римана на «сверхкоротких» промежутках критической прямой, то есть на промежутках 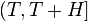, длина 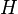которых растёт медленнее любой, даже сколь угодно малой, степени 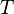. В частности, он доказал, что для любых заданных чисел , 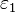с условием 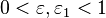почти все промежутк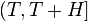и при 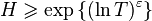содержат не менее нулей функции . 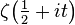Эта оценка весьма близка к той, что следует из гипотезы Римана.