Проекции геометрических тел

Для того, чтобы при выполнении чертежей представить себе форму детали удобно мысленно расчленять деталь на геометрические тела. Геометрические тела, ограниченные плоскими фигурами – многоугольниками, называют многогранниками (рис. 13). Их плоские фигуры называются гранями, а линии их пересечения – ребрами. Угол, образованный гранями, сходящимися в одной точке – вершине, будет многогранным углом. Например. Призма и пирамида – многогранники. Тела вращения ограничены поверхностями, которые получаются в результате вращения около оси какой-либо линии АВ, называемой образующей.

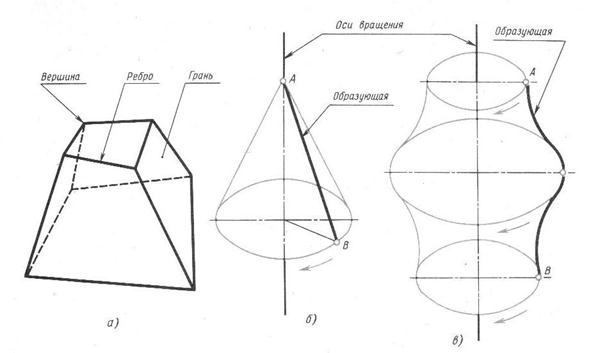
Рис. 13. Многогранные тела и тела вращения

Проекции призм

Построение проекции правильной прямой шестигранной призмы (рис. 14) начинается с выполнения ее горизонтальной проекции – правильного шестиугольника. Из вершин этого шестиугольника проводят вертикальные линии связи и строят фронтальную проекцию нижнего основания призмы. Эта проекция изображается отрезком горизонтальной прямой. От этой прямой вверх откладывают высоту призмы и строят фронтальную проекцию верхнего основания. Затем вычерчивают фронтальные проекции ребер – отрезки вертикальных прямых, равные высоте призмы. Фронтальные проекции передних и задних ребер совпадают. Горизонтальные проекции боковых граней изображаются в виде отрезков прямых.

Рис. 14. Проекция шестигранной призмы

Проекции пирамид

Построение проекций трехгранной пирамиды начинается с построения основания, горизонтальная проекция которого представляет собой действительный вид треугольника (рис.15). Фронтальная проекция основания изображается горизонтальным отрезком прямой. Из горизонтальной проекции s вершины пирамиды и получают фронтальную проекцию s’ вершины. Соединяя точку s’ с точками 1’, 2’ и 3’, получают фронтальные проекции ребер пирамиды.

Горизонтальные проекции ребер получают соединяя горизонтальную проекцию s вершины пирамиды с горизонтальными проекциями 1, 2 и 3 вершин основания.

Рис. 15. Проекции пирамиды

Проекции цилиндров

Боковая поверхность прямого кругового цилиндра образованна движением отрезка АВ вокруг вертикальной оси по направляющей окружности. На рис. 16,а дано наглядное изображение цилиндра. Построение горизонтальной и фронтальной проекций цилиндра показано на рис. 16,б и 16,в.

Рис. 16. Проекции цилиндра

Построение начинают с изображения основания цилиндра, т.е. двух проекций окружности. Т.к. окружность расположена на плоскости Н, то она проецируется на эту плоскость без искажения. Фронтальная проекция окружности представляет собой отрезок горизонтальной прямой линии, равный, равный диаметру окружности основания.

После построения основания на фронтальной проекции проводят две очерковые (крайне) образующие и на них откладывают высоту цилиндра. Проводят отрезок горизонтальной прямой, который является фронтальной проекцией верхнего основания цилиндра.

Проекции конусов.

Наглядное изображение прямого кругового конуса показано на рис. 17,а. Боковая поверхность конуса образованна вращением образующей BS около оси конуса по направляющей – окружности основания. Последовательность построения двух проекций конуса показана на рис. 17, б и в. Предварительно строят две проекции основания. Горизонтальная проекция основания – окружность. Если предположить, что основание конуса лежит на плоскости Н, то фронтальной проекцией будет отрезок прямой, равный диаметру этой окружности. На фронтальной проекции из середины основания восстанавливают перпендикуляр и на нем откладывают высоту конуса. Полученную фронтальную проекцию вершины конуса соединяют прямыми с концами фронтальной проекции основания и получают фронтальную проекцию конуса.

Рис. 17. Проекции конуса