Закон Гука

Цель работы: изучить виды деформации твердого тела и определить модули сдвига исследуемого материала.

Теоретическая часть

Деформация

В изолированном твердом теле (на тело не действуют никакие внешние силы) атомы находятся, в основном, в состоянии колебательного (теплового) движения относительно фиксированных в пространстве положений равновесия. Если к твердому телу приложить внешние силы так, чтобы выполнялись условия его статического равновесия (векторные суммы, как внешних сил, так и моментов внешних сил равны нулю) положения равновесия атомов в пространстве изменятся. При этом может измениться либо форма твердого тела, либо его объем, либо и форма и объем. Говорят, что тело под воздействием статических нагрузок тело деформируется. После прекращения воздействия внешних сил тело либо восстанавливает свою первоначальную форму и размеры, (такая деформацияназывается упругой), либо форма и размеры его не совпадают с первоначальными (при пластической деформации). Характер деформации зависит от величины внешних сил, от размеров и формы твердого тела, а также от свойств материала. Мы будем рассматривать лишь упругую деформацию.

Закон Гука

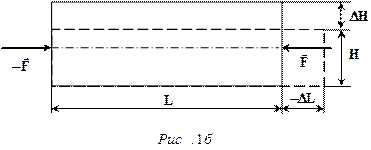Рассмотрим упругую деформацию, возникающую в стержне, т.е. теле, имеющем форму правильной призмы или цилиндра, при воздействии двух сил, равномерно распределенных по основаниям призмы и направленных вдоль оси стержня. Из условий статического равновесия (векторная сумма сил должна быть равна нулю) силы, приложенные к основаниям должны быть одинаковой величины и иметь противоположные направления. Статическое равновесие требует также равенства нулю момента внешних сил, что может быть выполнено в данном случае только при расположении сил вдоль одной прямой. Эта прямая перпендикулярна основаниям. Две возможных схемы приложения сил и соответствующие им деформации представлены на рис. 1а и рис. 1б.

Исходное (недеформированное) состояние стержня представлено пунктирными линиями. В случае, изображенном на рис. 1а стержень испытывает деформацию растяжения. Его длина Lувеличивается на величину DL, которая называется абсолютной деформацией. Одновременно происходит уменьшение поперечных размеров стержня. На рис. 1а символом H обозначен какой-либо поперечный размер стержня (например, диаметр для стержня цилиндрической формы или поперечный размер грани для стержня призматической формы). При растяжении стержня этот размер уменьшается на величину DH. Такую деформацию мы считаем отрицательной.

На рис. 1б представлена деформация стержня под действием сжимающих сил. В этом случае продольный размер L уменьшается на величину DL(абсолютная деформация равна -DL), а поперечный размер H увеличивается на величину DH( абсолютная деформация равна положительному числу +DH).

Для изотропных материалов (т.е. таких, у которых свойства одинаковы по всем направлениям) между поперечной и продольной деформациями существует следующее соотношение:

, (1)

в котором m¾ коэффициент Пуассона, зависящий от упругих свойств материала.

Величины отношений и называются относительной поперечной и относительной продольной деформациями, соответственно.

При небольших деформациях между модулем приложенной к стержню силы и величиной (модулем) относительной продольной деформации существует соотношение, называемое законом Гука:

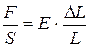, (2¢)

где S ¾ площадь поперечного сечения стержня, Е ¾ модуль Юнга, зависящий от упругих свойств материала. Величина отношения модуля силы, перпендикулярной сечению, к площади поперечного сечения называется нормальным напряжением, s. Физический смысл нормального напряжения аналогичен смыслу давления. Закон Гука часто записывают через нормальное напряжение:

(2)

Оказывается, упругие свойства изотропных материалов полностью описывается с помощью двух величин ¾ коэффициента Пуассона и модуля Юнга. Другими словами: деформации, возникающие в твердом теле произвольной формы при воздействии на него произвольной системы сил, удовлетворяющей условиям статического равновесия твердого тела, могут быть рассчитаны с помощью только этих двух постоянных. Рассмотрим справедливость этого утверждения на примере более сложных систем сил.