Всестороннее сжатие

Так называется деформация, возникающая в твердом теле, помещенном в среду с постоянным давлением (например, в газ). Рассмотрим деформацию всестороннего сжатия тела в форме прямоугольного параллелепипеда, имеющего размеры 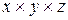. На все его грани действует одинаковое давление, которое и равно напряжению на гранях. Эти напряжения сжимают тело (см. рис. 2). На рисунке показаны оси координат и обозначены напряжения на гранях, перпендикулярных этим осям. Ось «OX» направлена вдоль грани параллелепипеда, имеющей размер х, ось «OY» ¾ вдоль грани с размером y. Очевидно, что при всестороннем сжатии . Обозначим эти равные друг другу напряжения через s.Поскольку закон Гука устанавливает линейную связь между напряжением и деформацией, для расчета деформации, вызванной несколькими напряжениями, можно использовать принцип суперпозиции. Рассмотрим применение этого принципа на примере вычисления деформации вдоль оси «ОХ». Эта деформация равна сумме деформаций, возникающих под действием напряжения 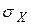, и независимо друг от друга. Пользуясь законом Гука, вычислим относительную деформацию , возникающую только под действием напряжения 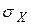: 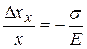. Напомним, что отрицательный знак деформации соответствует уменьшению размера.

Применяя закон Гука и используя связь между продольной и поперечной деформациями (1), вычислим относительную деформацию , порожденную только напряжением :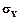

.

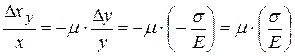Наконец, таким же способом найдем относительную деформацию , возникающую только под действием напряжения вдоль оси «OZ»:

.

Согласно принципу суперпозиции, полная относительная деформация вдоль оси «OX» равна:

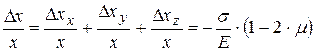
Таким же образом находим полные относительные деформации вдоль двух других осей координат:

,

.

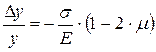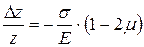Определим величину относительной объемной деформации при всестороннем сжатии , где V ¾ объем тела, а DV ¾ абсолютное изменение объема. 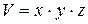, 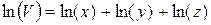. Найдем дифференциал логарифма объема: . При малых деформациях дифференциалы переменных можно заменить их приращениями. В результате получаем формулу для относительной объемной деформации:

.

Отсюда следует выражение для величины напряжения при объемной деформации:

,

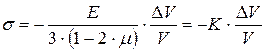где величина 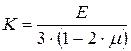называется модулем объемной деформации.