
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Чистое кручение
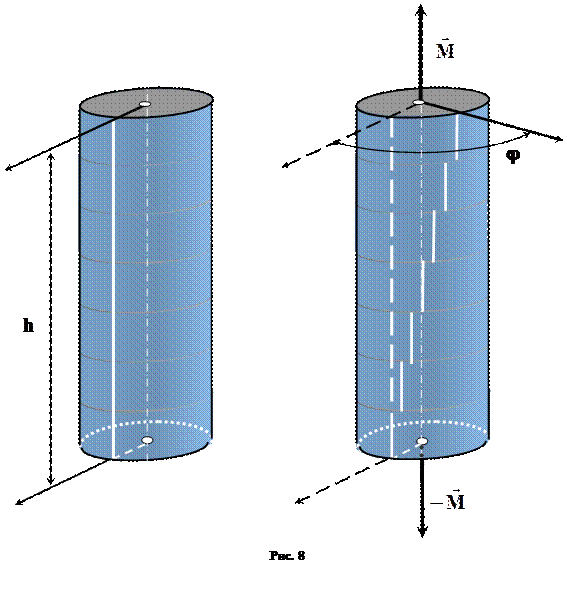
Рассмотрим деформацию чистого кручения на примере стержня, имеющего форму прямого кругового цилиндра. Такой вид деформации возникает при воздействии на торцы цилиндра двух равных по величине и противоположных по направлению моментов сил М, направленных вдоль оси цилиндра и равномерно распределенных по площади торцов. На рис. 8 показана деформация такого цилиндра. Ее можно представить, как совокупность взаимных поворотов бесконечно тонких слоев, на которые разделен цилиндр плоскостями, перпендикулярными своей оси. При чистом кручении слои остаются плоскими, т.е. сохраняют свою форму и размеры. Для наглядности на рисунке показаны слои достаточно большой толщины. Показан угол j, на который повернулся верхний торец цилиндра относительно нижнего. Этот угол является количественной мерой деформации чистого кручения и называется углом кручения. При упругой деформации чистого кручения закон Гука имеет вид:
 , (5)
, (5)
где величина f называется модулем кручения. Наша задача ¾ выразить модуль кручения.
 |
Рассмотрим равновесие верхнего цилиндрического слоя. Он находится под воздействием момента внешних сил
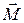 , приложенного к верхнему сечению слоя. К нижнему сечению этого слоя приложен момент сил упругости
, приложенного к верхнему сечению слоя. К нижнему сечению этого слоя приложен момент сил упругости 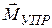 . В равновесии должно выполняться равенство
. В равновесии должно выполняться равенство  , из которого следует
, из которого следует  .
.
Рассмотрим деформацию бесконечно тонкого слоя цилиндра высотой dz. Его верхнее сечение повернулось на угол dj относительно нижнего. На рис. 9 показана ось «OZ» и положительный относительно этой оси угол dj. Показаны моменты сил упругости  и
и 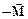 , действующие на рассматриваемый слой со стороны отброшенных частей цилиндра. Выделим внутри этого слоя бесконечно малый элемент объема, который
, действующие на рассматриваемый слой со стороны отброшенных частей цилиндра. Выделим внутри этого слоя бесконечно малый элемент объема, который  в недеформированном слое имел форму прямого прямоугольного параллелепипеда высотой dz с двумя гранями, расположенными перпендикулярно радиусу и двумя гранями, расположенными перпендикулярно радиусу цилиндра.
в недеформированном слое имел форму прямого прямоугольного параллелепипеда высотой dz с двумя гранями, расположенными перпендикулярно радиусу и двумя гранями, расположенными перпендикулярно радиусу цилиндра.
 После деформации все слои этого элемента объема сместятся параллельно основанию, т.е. этот элемент объема испытывает деформацию сдвига. Угол сдвига будет зависеть от угла кручения, расстояния элемента объема от оси цилиндра и высоты цилиндра, h. Найдем вид этой зависимости.
После деформации все слои этого элемента объема сместятся параллельно основанию, т.е. этот элемент объема испытывает деформацию сдвига. Угол сдвига будет зависеть от угла кручения, расстояния элемента объема от оси цилиндра и высоты цилиндра, h. Найдем вид этой зависимости.
На рис. 10 показаны размеры и форма рассматриваемого бесконечно малого (в дальнейшем б.м.) объема в недеформированном состоянии и после его деформации.
Обозначения на рисунке: dz ¾ толщина слоя, da ¾ угловой размер б.м. объема, r¾расстояние этого объема от оси цилиндра,  ¾ размер б.м. кубика в тангенциальном направлении, dr ¾ размер б.м. кубика в радиальном направлении, dj ¾ угловая деформация кручения цилиндрического слоя, g ¾ угловая деформация сдвига б.м. объема, D ¾ линейное перемещение верхней грани б.м. кубика относительно нижней при деформации сдвига, t ¾ касательные напряжения сдвига на гранях б.м. кубика, параллельных основаниям цилиндра (на двух других гранях имеются касательные напряжения той же величины, но они не показаны на рисунке).
¾ размер б.м. кубика в тангенциальном направлении, dr ¾ размер б.м. кубика в радиальном направлении, dj ¾ угловая деформация кручения цилиндрического слоя, g ¾ угловая деформация сдвига б.м. объема, D ¾ линейное перемещение верхней грани б.м. кубика относительно нижней при деформации сдвига, t ¾ касательные напряжения сдвига на гранях б.м. кубика, параллельных основаниям цилиндра (на двух других гранях имеются касательные напряжения той же величины, но они не показаны на рисунке).
 Выразим угловую деформацию кручения dj через угол кручения цилиндра j. Поскольку все бесконечно тонкие слои одинаковой толщины dzиспытывают воздействие одинаковых скручивающих моментов сил, их деформации djодинаковы. Отсюда вытекает, что угол кручения цилиндра, имеющего высоту h,равен произведению djна количество слоев толщинойdz,т.е.
Выразим угловую деформацию кручения dj через угол кручения цилиндра j. Поскольку все бесконечно тонкие слои одинаковой толщины dzиспытывают воздействие одинаковых скручивающих моментов сил, их деформации djодинаковы. Отсюда вытекает, что угол кручения цилиндра, имеющего высоту h,равен произведению djна количество слоев толщинойdz,т.е.  . Откуда
. Откуда  .
.
Найдем теперь угловую деформацию сдвига g. Для этого выразим линейное смещение верхней грани D,с одной стороны, через g, а с другой ¾ через dj:  . Отсюда
. Отсюда  . Вычислим момент сил упругости через касательные напряжения t. Используем закон Гука для деформации сдвига (4) и получаем:
. Вычислим момент сил упругости через касательные напряжения t. Используем закон Гука для деформации сдвига (4) и получаем:  . К грани кубика с площадью
. К грани кубика с площадью  приложена касательная сила
приложена касательная сила 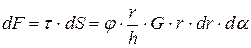 . Проекция момента этой силы на ось «OZ» равна
. Проекция момента этой силы на ось «OZ» равна  . Интегрируя по площади верхнего сечения цилиндрического слоя, получаем
. Интегрируя по площади верхнего сечения цилиндрического слоя, получаем  (через
(через  обозначен внешний радиус цилиндра).
обозначен внешний радиус цилиндра).
Проекция момента внешних сил на ось «OZ», т.е. М, приложенных к верхнему сечению всего цилиндра, равна найденной проекции момента сил упругости:
 (6)
(6)
Сравнивая это выражение с формулой (5), находим выражения для модуля кручения:
 (7)
(7)
Дата добавления: 2015-04-11; просмотров: 264; Мы поможем в написании вашей работы!; Нарушение авторских прав |