
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Внутренние силовые факторы при кручении
Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор - крутящий момент.
Внешними нагрузками также являются две противоположно натравленные пары сил.
Рассмотрим внутренние силовые факторы при кручении круглого бруса (рис. 26.1).
Для этого рассечем брус плоскостью I и рассмотрим равновесие сеченной части (рис. 26.1а). Сечение рассматриваем со стороны отброшенной части.
Внешний момент пары сил разворачивает участок бруса против часовой стрелки, внутренние силы упругости сопротивляются повороту. В каждой точке сечения возникает поперечная сила dQ рис. 26.16). Каждая точка сечения имеет симметричную, где возникает поперечная сила, направленная в обратную сторону. Эти силы разуют пару с моментом dm=pdQ; p — расстояние от точки до центра сечения. Сумма поперечных сил в сечении равна нулю: ΣdQ = 0.
С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим моментом:
 .
.
Практически крутящий момент определяется из условия равновесия отсеченной части бруса.
Крутящий момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (рис. 26.1в):
 , т.е.
, т.е.  ;
; 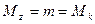 .
.
Дата добавления: 2015-04-11; просмотров: 462; Мы поможем в написании вашей работы!; Нарушение авторских прав |