Напряжение в любой точке поперечного сечения

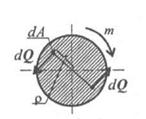Рис.	Рассмотрим поперечное сечение круглого бруса. Под действием внешнего момента в каждой точке поперечного сечения возникают силы упругости dQ (рис. 27.2). dQ = τdA, где τ — касательное напряжение; dA — элемен­тарная площадка. В силу симметрии сечения силы dQ образуют пары.

Элементарный момент силы dQ относительно центра круга

dm = pdQ,

где р — расстояние от точки до центра круга.

Суммарный момент сил упругости получаем сложением (интегрированием) элементарных моментов:

.

После преобразования получим формулу для определения напря­жений в точке поперечного сечения:

, где .

При ρ = 0 τ_к = 0; касательное напряжение при кручении пропорционально расстоянию от точки до центра сечения. Полученный интеграл J_p называется полярным моментом инерции сечения. J_р является геометрической характеристикой сечения при кручении. Она характеризует сопротивление сечения скручиванию.

Анализ полученной формулы для J_р показывает, что слои, рас­положенные дальше от центра, испытывают большие напряжения.

Эпюра распределения касательных напряжений при кручении (рис. 27.3)

Мк — крутящий момент в сечении; ρВ — расстояние от точки В доцентра; τВ — напряжение в точке В; — максимальное напря­жение.

Рис.