
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Последовательно по участкам нагружения рассматриваем внутренние силовые факторы в сечениях
Последовательно по участкам нагружения рассматриваем внутренние силовые факторы в сечениях. Силовые факторы определяем из условий равновесия отсеченной части. Для каждого участка записываем уравнения внутренних силовых факторов.
Используем известные правила:
- поперечная сила численно равна алгебраической сумме проекций внешних сил на ось Оу;
- изгибающий момент численно равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть, относительно нейтральной оси, совпадающей с осью Ох;
- принятые знаки поперечных сил и изгибающих моментов (рис. 30.2):

Рис.
Составим уравнения равновесия.
1. Рассмотрим участок 1 (рис. 30.3а).
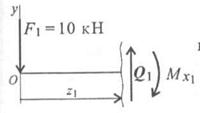 Рис.
Рис.
| 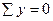 ; ;  ; ;  ; ;  .
Сила Q1 – отрицательная. Сила Q на участке 1 постоянна. .
Сила Q1 – отрицательная. Сила Q на участке 1 постоянна.
 ; ;  ; ;  .
Мх – отрицательный.
0 ≤ z1 ≤ 3 м:
при z1 = 0; Мх0 = 0;
при z1 = 3 м; МхА = - 30 кН. .
Мх – отрицательный.
0 ≤ z1 ≤ 3 м:
при z1 = 0; Мх0 = 0;
при z1 = 3 м; МхА = - 30 кН.
|
Изгибающий момент меняется по линейному закону, график – прямая линия.
2. Рассмотрим участок 2 (рис. 30.3б).
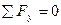 ;
; 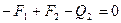 ;
;
 ;
;
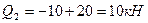 .
.
Сила Q2 положительна.
 ;
;
 ;
;
 Рис.
Рис.
|  . .
 :
при z2 = 3 м
МхА = 10 · 3 = 30 кН·м;
Мх – отрицательный;
при z2 = 7 м :
при z2 = 3 м
МхА = 10 · 3 = 30 кН·м;
Мх – отрицательный;
при z2 = 7 м
 . .
|
Знак сменился; МхВ слева определять сразу из зависимостей 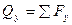 ;
;  , не составляя уравнения равновесия участка.
, не составляя уравнения равновесия участка.
Закон каждого из слагаемых этих уравнений определяем отдельно (участок 3).
3. Рассмотрим участок 3 (рис. 30.3в).
 - положительна. - положительна.
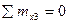 ; ; 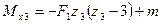 .
7 м ≤ z3 ≤ 10 м:
при z3 = 7 м .
7 м ≤ z3 ≤ 10 м:
при z3 = 7 м
 ;
при z3 = 10 м ;
при z3 = 10 м
 . .
|  Рис.
Рис.
|
Обращаем внимание, что для точки В получено два значения изгибающих моментов: из уравнения для участка 2 левее точки В и из уравнения для участка 3 — правее точки В.
Это объясняется тем, что именно в этой точке приложен внешний момент и поэтому внутренний момент сил упругости меняется.
В точках приложения внешнего момента на эпюре моментов появится скачок, равный величине приложенного момента.
Поперечная сила в точке В для второго и третьего участков одинакова. Следовательно, приложение внешнего момента не отражается на эпюре поперечных сил. График поперечной силы на участке 3 — прямая линия.
График изменения изгибающих моментов на третьем участке также прямая линия.
4. Построение эпюр. Порядок построения эпюр остается прежним: масштабы эпюр выбираются отдельно, исходя из значений максимальных сил и моментов.
Графики обводятся толстой основной линией и заштриховываются поперек. На графиках указываются значения поперечных сил, изгибающих моментов и единицы измерения.
Правила построения эпюр (рис. 30.1 и 30.4):
1. Для участка, где отсутствует распределенная нагрузка, поперечная сила постоянна, а изгибающий момент меняется по линейному закону.
2. В частном случае, когда поперечная сила на участке равна нулю, изгибающий момент постоянен (чистый изгиб), график - прямая линия, параллельная продольной оси (на рис. 30.1 отсутствует).
3. В том месте, где к балке приложена внешняя сосредоточенная сила, на эпюре Q возникает скачок на величину приложенной силы, а на эпюре моментов - излом.
4. В сечении, где к балке приложена пара сил (сосредоточенный момент), а эпюре Ми возникает скачок на величину момента этой пары. Поперечная сила при этом не изменяется.
5. В сечении на конце балки поперечная сила равна приложенной в этом сечении сосредоточенной силе или реакции в заделке.
6. На свободном конце балки или шарнирно опертом конце момент равен нулю, за исключением случаев, когда в этом сечении приложена пара сил (внешний момент).
Пример 2.На двухопорную балку действуют сосредоточенные силы и моменты (рис. 30.4). Построить эпюры поперечных сил иизгибающих моментов.
Для двухопорной балки построение эпюр начинают с определения опорных реакций балки. Для их определения используем систему уравнений равновесия, составляем два уравнения моментов относительно шарнирных опор. Затем проводим проверку правильности решения по уравнению 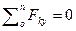 .
.
Дата добавления: 2015-04-11; просмотров: 334; Мы поможем в написании вашей работы!; Нарушение авторских прав |