Решение. 1. Определение реакций в опорах

1. Определение реакций в опорах. Уравнения равновесия:

; ;

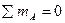- 35 ·6 + 80 – R_B · 10 + 70 · 12 = 0;

R_B · 10 = - 210 + 80 + 840;

R_B = 71 кН.

; R_A · 10 + F₁ · 4 + m + F₂ · 2 = 0;

R_A · 10 + 80 + 35 · 4 + 70 · 2 = 0$

R_A · 10 = - 80 – 140 – 140 = - 360$

R_A = - 36 кН.

Рис.

Реакция в опоре направлена в обратную сторону.

Проверка: ΣF_y = 0;

- R_A + F₁ + R_B – F₂ = 0; - 36 + 35 + 71 – 70 = 0.

Реакции определены верно.

2. Для упрощения расчетов при построении эпюр поперечных сил и изгибающих моментов можно провести расчет по характерным точкам без составления уравнений.

Для этого используют известные связи между поперечной силок и изгибающим моментом и правила построения эпюр.

Участок 1 (от точки А до точки С).

В точке А приложена реакция Ra, направленная вниз. Попереч­ная сила на участке постоянна: Q₁ = R_a = - З6 кН.

Момент в точке А равен нулю.

Точка С (слева). Приложена внешняя сила F₁ = 35кН, напра­вленная вверх, - здесь возникнет скачок вверх на величину 35 кН. Момент в точке С (слева) может быть рассчитан по известной зави­симости ; .

Участок 2 (от точки С справа до точки В).

Поперечная сила в точке С (справа) равна Qc = - R_А + F₁;

Q_c = - 36 + 35 = - 1 kH.

В точке С приложена внешняя пара сил с моментом 80 кН·м, следовательно, здесь проявляется скачок на величину приложенного момента: ; .

Поперечная сила на втором участке постоянна: .

Момент в точке В определяется по зависимости

; .

Справа и слева от точки В момент имеет одинаковые значения.

Участок 3 (от точки В (справа) до точки D).

В точке В приложена внешняя сила R_В. Здесь появляется скачок на величину 71 кН, Q_b = -1 + 71 = 70 кН.

Дальше по участку поперечная сила не изменяется. Момент в точке D равен нулю, т.к. здесь не приложена внешняя пара сил: M_D = 0.

Рассмотрение поперечных сил и изгибающих моментов можно было провести и справа налево.

По полученным значениям сил и моментов строим эпюры (эпю­ры под схемой вала, рис. 30.4).

Контрольные вопросы и задания

1. Определите величины поперечных сил в сечении 1 и в сече­нии 2 (рис. 30.5).

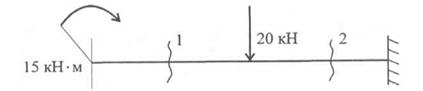
Рис.

2. Напишите формулу для расчета изгибающего момента в сечении 3 (рис. 30.6).

Рис.

3. Из представленных эпюр выберете эпюру поперечной силы
для изображенной балки (рис. 30.7).

Пояснения.

A. Обратить внимание на знак силы в сечении 1 (знак +).

Б. Обратить внимание на величину скачков в местах приложе­ния внешних сил.

B. Приложение момента пары сил не должно отражаться на эпюре Q.

4. По рис. 30.8 выбрать эпюру изгибающего момента для изображенной на рис. 30.7 балки.

Рис.

Рис.

Пояснения.

A. На конце бруса приложен момент пары, следовательно, в этом месте изгибающий момент должен быть равен этому же значению.

Б. Обратить внимание на знак момента в сечении 1.

B. В точке А приложена также и сила, поэтому линия, очертившая эпюру, должна быть наклонной.