Основные законы алгебры логики

1) Законы нулевого множества:

, , ,

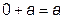т.е. конъюнкция любого числа переменных обращается в ноль, если хотя бы одна переменная имеет значение 0, независимо от значений других переменных.

2) Законы универсального множества:

, , ,

т.е. дизъюнкция любого числа переменных обращается в единицу, если хотя бы одна переменная имеет значение 1, независимо от значений других переменных.

3) Законы идемпотентности (повторения, тавтологии):

, .

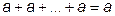4) Закон двойной инверсии:

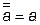, т.е. двойную инверсию можно снять.

5) Законы дополнительности:

закон логического противоречия

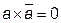, т.е. конъюнкция любой переменной и ее инверсии есть 0;

закон исключенного третьего

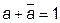, т.е. дизъюнкция любой переменной и ее инверсии есть 0.

6) Коммутативные законы (законы перемещения):

,

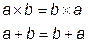т.е. результаты выполнения операции конъюнкции и дизъюнкции не зависят от того, в каком порядке следуют переменные.

7) Ассоциативные законы (законы сочетания):

,

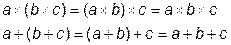т.е. для записи конъюнкции или дизъюнкции скобки можно опустить.

8) Дистрибутивные законы (законы распределения):

конъюнкции относительно дизъюнкции:

;

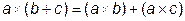дизъюнкции относительно конъюнкции:

.

9) Законы поглощения:

, .

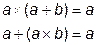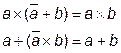10)Законы склеивания (распространения):

, .

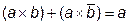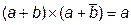11)Законы де Моргана (законы инверсии):

для двух переменных:

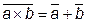, т.е. инверсия конъюнкции есть дизъюнкция инверсий;

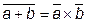, т.е. инверсия дизъюнкции есть конъюнкция инверсий;

в общем виде:

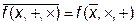или ,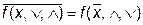

т.е. инверсия функции есть функция от инверсий её аргументов и операций дизъюнкции и конъюнкции.