
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формы описания логических функций
Для описания ФАЛ могут быть использованы разные способы. Основными из них являются описание ФАЛ в словесной форме, в виде таблиц истинности, последовательности десятичных чисел, а также алгебраических выражений:
1) Словесное описание ФАЛ применяется для первичного описания поведения логического устройства.
Пример словесного описания ФАЛ: «Логическая функция трех переменных равна единице, если хотя бы две переменные равны единице».
2) Описание ФАЛ в виде таблиц истинности. Таблица, которая содержит все возможные комбинации входных переменных xn–1,…,x1,x0 и соответствующие им значения выходных переменных yi, называется таблицей истинности или комбинационной таблицей. В общем (полном) случае таблица содержит 2n строк.
Пример таблицы истинности для ФАЛ трех переменных:
| x2 | x1 | x0 | y = f(x2,x1,x0) |
3) Описание ФАЛ в виде последовательности десятичных чисел. При таком описании последовательно записывают десятичные эквиваленты двоичных кодов входных переменных, которые соответствуют значению ФАЛ равному «0» или «1».
Пример описания для ФАЛ заданной приведенной выше таблицей истинности:
F(x2,x1,x0) = S(1,2,4,7) = Ú(1,2,4,7) или F(x2,x1,x0) = P(0,3,5,6) = Ù(0,3,5,6).
4) Описание ФАЛ в виде алгебраических выражений. Алгебра логики позволяет создавать сложные функции, аргументы которых являются функциями других двоичных аргументов. Операция замены аргументов одной функции другими, более простыми функциями называется суперпозицией функции. Многоразовое использование принципа суперпозиции дает возможность получить функции желательного числа аргументов.
Элементарная конъюнкция получается конъюнкцией конечного множества логических переменных и их инверсий.
Пример:  .
.
Элементарная дизъюнкция получается дизъюнкцией конечного множества логических переменных и их инверсий.
Пример:  .
.
Дизъюнкция любого числа элементарных конъюнкций называется дизъюнктивной нормальной формой ФАЛ (ДНФ).
Пример:  .
.
Конъюнкция любого числа элементарных дизъюнкций называется конъюнктивной нормальной формой ФАЛ (КНФ).
Пример:  .
.
Логическую функцию, заданную любым аналитическим выражением, можно непосредственно преобразовать в ДНФ или КНФ, используя законы де Моргана (законы инверсии) и дистрибутивные законы.
Если в состав логического выражения входят наборы элементарных конъюнкций с одинаковым количеством переменных, связанные дизъюнкцией, то такая форма ФАЛ называется совершенной ДНФ (СДНФ).
Если в состав логического выражения входят наборы элементарных дизъюнкций с одинаковым количеством переменных, связанные конъюнкцией, то такая форма ФАЛ называется совершенной КНФ (СКНФ).
Пример построения СДНФ и СКНФ:
Рассмотри функцию, заданную приведенной выше таблицей истинности:
| Значения аргументов | Значения функции | СДНФ | СКНФ | ||
| x2 | x1 | x0 | y = f(x2,x1,x0) | ||

| |||||

| – | ||||
| – | 
| ||||
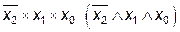
| – | ||||
| – | 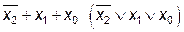
| ||||
| – | 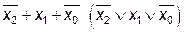
| ||||
| – | 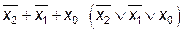
| ||||

| – |
СДНФ: 
СКНФ: 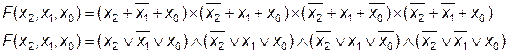 .
.
Дата добавления: 2015-04-11; просмотров: 300; Мы поможем в написании вашей работы!; Нарушение авторских прав |