Внешние

возмущенияОграничения

- экономические; - временные;

- технологические; - финансовые;

- политические; - нормативно-правовые;

- экологические; - логистические;

- конкурентные - качественные

ПРОЕКТ

социально-

экономические

потребности степень

удовлетворенности

потребностей

ОБЕСПЕЧЕНИЕ:

- кадровое

- технологическое

- материально-техническое

- энергетическое

- инструментальное

- информационное

- и др.

Рис. 1.18. Системная модель проекта

, , (1.1)

где 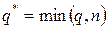; ; 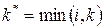– число различных структурных конфигураций, содержащих i каналов без установления в них видов связей; – число различных видов связей, допустимых в -м канале при р-й конфигурации.

Формула (1.1) и более общие, полученные на ее основе для определения числа различных структур в системах любой сложности и приведенные в работе [8], решают задачу перечисления структур сложных проектов и программ, т. е. составлять списки с указанием в структуре числа задействованных элементов, каналов связи и видов связи.

Где 1 .2. Решение задачи перечисления структур проектов позволяет перейти к рассмотрению задачи структурной оптимизации. Здесь, по-видимому, возможны два различных подхода. Первый состоит в прямом использовании сетевых методов оптимизации. С этой целью, опираясь на результаты перечисления структур, для каждой структуры необходимо определить смежные, т.е. те структуры, в которые возможен непосредственный переход. После оценки «стоимости» перехода нетрудно построить сеть структурных переходов, узлами которой будут структуры. Далее, исходя из критериев эффективности проекта, структурную оптимизацию можно осуществить различными хорошо известными методами. Сложность и трудоемкость такого подхода очевидна. Более продуктивен другой подход, основанный на идее метризации множества структур с числом элементов S, полученного в результате перечисления структур.

Введем в рассмотрение следующую функцию расстояния между структурами

, (1.2)

где – критерий, в общем случае векторный, эффективности проекта при структуре и управляющих параметрах проекта u; U – допустимое множество управляющих параметров.

Пространство структур , представляющее собой прямое произведение множества структур, путем введения функции по формуле (1.2) становится метрическим. Это следует из того, что при отождествлении структур с одинаковыми функциональными возможностями функция удовлетворяет аксиомам метрического пространства, т.е. следующим трем условиям:

1. Тождества, тогда и только тогда, когда .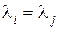

2. Симметрии, .

Первые два условия очевидны.

3. Неравенству треугольника, .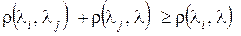

Действительно,

.

.

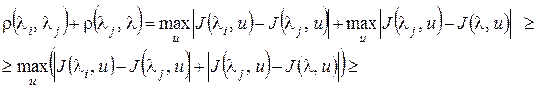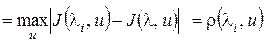Функция позволяет различать структуры проекта не с точки зрения ее состава, а с точки зрения возможных результатов. Данное обстоятельство нередко приводит к существенному сокращению числа рассматриваемых структур. Все , для которых , можно отождествить. Метризация множества структур дает возможность применять методы последовательного анализа вариантов для структурной оптимизации.

Пусть процесс реализации проекта происходит на интервале 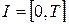. Обозначим через 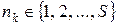значение целочисленной функции на частичном интервале , определяющее выбор структуры на -м интервале. Этим значениям будет отвечать множество значений критерия 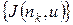, что позволяет дать оценку эффективности проекта за весь период функционирования Т в виде

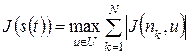, (1.3)

где равно 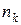на частичном интервале .

Выделим среди множества структур структуру

,

обладающую минимальными критериальными возможностями при наиболее эффективных значениях управляющих параметров. Если таковых несколько, то будем считать их эквивалентными. Пользуясь формулой (1.2), упорядочим структуры множества , перенумеровав их в порядке возрастания расстояния до . При этом структуры с одинаковыми расстояниями будем отождествлять. Получим множество структур , для которых , если .

Заметим, что практически все реальные проекты содержат структуру , для которой при . В этом случае расстояние будет адекватно критериальным возможностям структуры . Кроме того, условие всегда можно обеспечить, вводя соответствующее нормирование критерия.

Теперь для структурной оптимизации проекта в соответствии с критерием (3) можно воспользоваться практически любым методом последовательного перебора и анализа вариантов. Рассмотрим, например, применение метода локальных вариаций для определения структурного управления , оптимизирующего критерий (3). В соответствии с этим методом выбирается нулевое приближение . Вычисляется значение по формуле (1.3). В плоскости на прямых точками фиксируются все числовые значения элементов упорядоченного множества от 1 до S и строится ломанная линия, отвечающая функции . Затем, в определенной последовательности слева на право рассматриваются локальные вариации функции . А именно, последовательно на каждом частичном интервале варьируются целочисленные значения . Совокупность всех указанных вариаций на интервале I, приводящая к более предпочтительному по сравнению с значению критерия, определит первое приближение структурного управления к оптимальному и т.д. В результате, на некотором шаге вариаций улучшение критерия окажется невозможным. В этом случае структурное управление будет отвечать локальному экстремуму критерия (1.3).

3. В случае, если связи в структурах проекта носят неопределенный характер, то процедура структурной оптимизации несколько усложняется за счет необходимости учета дополнительного фактора – неопределенности связей. Такой учет может быть осуществлен путем включения в критерий оценки эффективности проекта показателя неопределенности. В качестве такового целесообразно, как меру неопределенности, ввести понятие энтропии структуры .

Согласно формуле (1.1) числовое значение индекса определяет число задействованных в соответствующих структурах каналов связи. Если неопределенность носит вероятностный характер, то известна или задается вероятность появления -го канала связи. Энтропия такой структуры определится по известной формуле.

.

Если неопределенность связи носит нечеткий характер, то для каждого канала необходимо на основе экспертных или статистических данных определить функции принадлежности , пользуясь, например, приведенными в работе [9] методиками. Затем эти функции следует пронормировать по формуле

и определить энтропию структуры , содержащей i каналов связи,

.

Более сложная ситуация с оценкой неопределенности связей возникает в случае изменения характера и степени неопределенности связи во времени. Такая ситуация также может быть проанализирована на основе изложенного подхода.

В заключение отметим следующее:

1. Изложенный метод структурного анализа носит достаточно общий характер. Он применим для проектов и программ любого уровня сложности.

2. Метод предоставляет дополнительные возможности для рациональной структуризации проектов и программ как на этапе прединвестиционного анализа, так и в процессе их реализации.

3. Введенный критерий эффективности проекта с учетом неопределенности связей позволяет осуществлять сравнительный анализ различных вариантов проектных решений.

Конструктивное развитие методов структурного анализа сложных проектов и программ видится в направлении формирования алгебраических структур на множестве структур проектов таких как полугруппа, моноид, группа и другие. При этом следует изучить возможность в ходе алгебраических операций выявлять наиболее рациональные структуры.