Вычисление объёмов тел вращения

Объём тела, образованного вращением вокруг оси ох криволинейной трапеции, ограниченной непрерывной линией , отрезком оси абсцисс и прямыми , вычисляется по формуле

.

Объём тела, образованного вращением вокруг оси оу криволинейной трапеции, ограниченной непрерывной линией 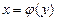, отрезком оси ординат и прямыми , вычисляется по формуле

.

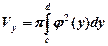Пример:Вычислить объём тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями

Построим ограничивающие линии.

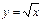- ветвь параболы, расположенная выше оси OX, т.к. ;

- прямая, параллельная оси OY;

- ось OX.

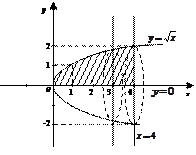
Рис. 11.

При вращении криволинейной трапеции (рис.11) вокруг оси ох образуется тело вращения.

Т. к. по условию криволинейная трапеция вращается вокруг оси ох, то объём тела вращения вычислим по формуле .

По условию , т.е. , тогда При этом , т.е.

Тогда (ед³.)

Пример:Вычислить объём тела, образованного вращением вокруг оси оу фигуры, ограниченной линиями

Построим ограничивающие линии.

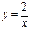- гипербола, ветви которой расположены в I и III координатных углах;

- прямая, параллельная оси OX;

- прямая, параллельная оси OX;

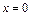- ось OY.

Рис. 12.

При вращении криволинейной трапеции (рис.12) вокруг оси оу образуется тело вращения.

Т.к. по условию криволинейная трапеция вращается вокруг оси оу, то объём тела вращения вычислим по формуле .

По условию , т.е. , тогда .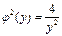

При этом , т.е. .

Тогда

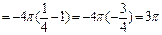(ед³.)

Пример:Вычислить объём тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями

Построим ограничивающие линии.

- парабола с вершиной в точке , симметрична относительно оси OY;

- парабола с вершиной в точке , симметрична относительно оси OX.

- прямая, параллельная оси OX;

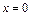- ось OY.

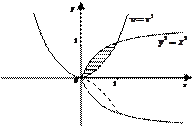
Рис. 13.

При вращении криволинейной трапеции (рис.13) вокруг оси OX образуется тело вращения.

По условию фигура вращается вокруг оси OX. Тогда искомый объём равен разности двух объёмов: объёма V_x1, полученного от вращения вокруг оси OX фигуры, ограниченной линиями и объёма V_x2, полученного от вращения вокруг оси OX фигуры, ограниченной линиями Т.о.

Вычислим .

Для V_x1: , при этом . Тогда

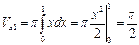(ед³.)

Вычислим .

Для V_x2: ,т. е Тогда (ед³.)

Т.о. 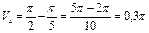(ед³.)