ТОЧЕЧНАЯ ОЦЕНКА СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Предположим, что генеральная совокупность является нормальным распределением. Нормальное распределение полностью определено математическим ожиданием (средним значением) и средним квадратичным отклонением. Поэтому, если по выборке можно оценить, т.е. приближенно найти, эти параметры, то будет решена одна из задач математической статистики – определение параметров большого массива по исследованию его части.

Параметры генеральной совокупности можно указать по параметрам выборки с учетом ее объема n.

Если считать, что статистическое распределение является выборкой из некоторой генеральной совокупности, при этом , то можно заключить, что для этой генеральной совокупности приближенно:

ИНТЕРВАЛЬНАЯ ОЦЕНКА. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ. ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ.

,

При достаточно большом объеме выборки можно сделать вполне надежные заключения о параметрах генеральной совокупности. Однако на практике часто имеют дело с выборками небольшого объема (n<30). При небольшом объеме выборки пользуются интервальными оценками. В этом случае указывается интервал (доверительный интервал).

Доверительный интервал – интервал, в котором с заданной доверительной вероятностью находится истинное значение случайной величины (среднее значение генеральной совокупности).

Доверительная вероятность – вероятность, с которой в заданном интервале (доверительном интервале) находится истинное значение случайной величины (среднее значение генеральной совокупности). Обычно в медико-биологических исследованиях доверительную вероятность принимают равной 0,95.

Доверительный интервал математически записывают так:

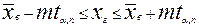, или

, где

- коэффициент Стьюдента (величина табличная, размерности не имеет),

a - доверительная вероятность,

n – объем выборки;

m – ошибка среднего.

Чтобы определить доверительный интервал, необходимо:

1. Вычислить среднее значение выборки ;

2. Вычислить дисперсию для выборки ;

3. Вычислить исправленную выборочную дисперсию:

4. Вычислить ошибку среднего .