
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
КОРРЕЛЯЦИОННАЯ ЗАВИСИМОСТЬ. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ И ЕГО СВОЙСТВА. УРАВНЕНИЯ РЕГРЕССИИ.
ЗАДАЧА корреляционного анализа сводится к:
1. Установлению направления и формы связи между признаками;
2. Измерению ее тесноты.
Функциональнойназывается однозначная зависимость между переменными величинами, когда определенному значению одной (независимой) переменной х, называемой аргументом, соответствует определенное значение другой (зависимой) переменной у, называемой функцией. (Пример: зависимость скорости химической реакции от температуры; зависимость силы притяжения от масс притягивающихся тел и расстояния между ними).
Корреляционной называется зависимость между переменными, имеющими статистистический характер, когда определенному значению одного признака (рассматриваемого в качестве независимой переменной) соответствует целый ряд числовых значений другого признака. (Пример: связь между урожаем и количеством осадков; между ростом и весом и т.д.).
Поле корреляции представляет собой множество точек, координаты которых равны полученным на опыте парам значений переменных х и у.
По виду корреляционного поля можно судить о наличии или отсутствии связи и ее типе.

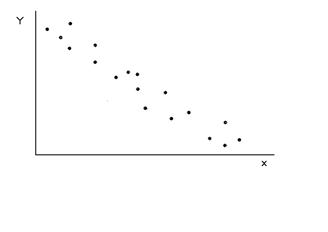
| Связь между величинами х и у линейная, положительная (прямая). | Связь между величинами х и у линейная, отрицательная (обратная). |


| Связь между величинами квадратичная. | Связи между величинами нет. |
Связь называется положительной, если при увеличении одной переменной увеличивается другая переменная.
Связь называется отрицательной, если при увеличении одной переменной уменьшается другая переменная.
Связь называется линейной, если ее можно в аналитическом виде представить как 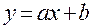 .
.
Показателем тесноты линейной связи является коэффициент линейной корреляции. Эмпирический коэффициент линейной корреляции определяется выражением:
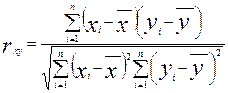
Коэффициент линейной корреляции лежит в пределах от -1 до 1 и характеризует степень близости между величинами x и y. Если:
1. 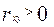 - положительная корреляция;
- положительная корреляция;
2. 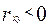 - отрицательная корреляция;
- отрицательная корреляция;
3.  - связь функциональная;
- связь функциональная;
4.  - связь высокая (или сильная);
- связь высокая (или сильная);
5.  - связь средняя;
- связь средняя;
6. 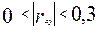 - связь слабая;
- связь слабая;
7. 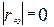 - линейной связи нет.
- линейной связи нет.
Корреляционную зависимость между признаками можно описывать разными способами. В частности, любая форма связи может быть выражена уравнением общего вида  . Уравнение вида
. Уравнение вида 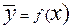 и
и 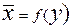 называются регрессией. Уравнение прямой регрессии у на х в общем случае можно записать в виде
называются регрессией. Уравнение прямой регрессии у на х в общем случае можно записать в виде

Уравнение прямой регрессии х на у в общем случае выглядит как

Наиболее вероятные значения коэффициентов а и в, с и d могут быть вычислены, например, при использовании метода наименьших квадратов.
Дата добавления: 2015-04-11; просмотров: 335; Мы поможем в написании вашей работы!; Нарушение авторских прав |