
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Условной вероятностью называют вероятность события А , вычисленную в предположении, что событие А свершилось. событие А свершилось.
56.Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже свершилось Р( АВ) =Р(А) 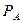 (В)
(В)
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.если появление одного из них не исключает появление другого в одном и том же испытании.
58.Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления Р (А+В) = Р(А) + Р(В) –Р( АВ). Р (А+В) = Р(А) + Р(В) –Р( АВ).
59.Вероятность появления события А , которое может наступить лишь при появлении одного из несовместных событий 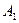 ,
,  ,…,
,…, 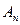 , образующих полную группу событий , равна сумме произведений вероятностей каждого из этих событий на соответствующую вероятность события А:Р( А) = Р (
, образующих полную группу событий , равна сумме произведений вероятностей каждого из этих событий на соответствующую вероятность события А:Р( А) = Р ( 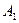 )
) 
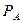 ( А ) + Р (
( А ) + Р (  )
)  (А) + Р (
(А) + Р ( 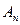 )
) 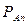 ( А ). Р( А) = Р (
( А ). Р( А) = Р ( 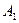 )
) 
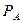 ( А ) + Р (
( А ) + Р (  )
)  (А) + Р (
(А) + Р ( 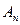 )
) 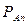 ( А ).
( А ).
60.Формула Байеса: 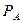 (
( 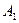 )= Р(
)= Р( 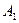 )
)  (А)/ Р(А)
(А)/ Р(А)
61.Формула Бернулли:  =
= 
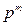

62.Локальная теорема Муавра – Лапласа: В случае, если число испытаний п велико, а вероятность появления события А постоянна и отлична от нуля, то вероятность того, что событие А в серии из n испытаний произойдет ровно m раз приближенна равна значению функции:  =
=  f(х), где f(х) =
f(х), где f(х) = 


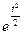 , t =
, t = 
63.Формула Пуассона:  =
=  e
e  ,
, 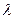 = np.
= np.
64.Интегральной теореме Лапласа: Р (  ,
,  ) =
) =  ( Ф(
( Ф( 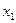 )-Ф(
)-Ф(  )), Ф(х)=
)), Ф(х)= 
 ,
, 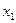 =
= 
Дата добавления: 2015-04-11; просмотров: 223; Мы поможем в написании вашей работы!; Нарушение авторских прав |