Рядом распределения называется совокупность всех возможных значений и соответствующих им вероятностей .

67.Значение функции распределения F(Х) при данном задании х равно вероятности того, что случайная величина Х примет значение меньшее х. F(Х)= Р( Х< х).

68.Свойство функции распределения. Если 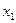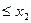, то 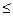F(х ) F(х )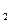

69.Свойство функции распределения. F(x) = 1

70.Вероятность попадания случайной величины в заданный интервал определяется по формуле Р (х ) = F(x )- F(x ).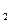

71.Математическое ожидание случайной величины Х обозначается М(Х) и определяется по формуле: М(Х) = .

72.Свойства М(Х): Если С- постоянная величина, то: М(С)=С, в частности, М(М(Х))= М(Х)

73.Свойство М(Х): Если У – случайная величина, то : М(Х+У)= М(Х)+М(У).

74.Свойство М(Х): Если У – случайная величина, то: М(Х-У)= М(Х) – М(У).

75.Свойство М(Х): Если У – случайная величина, то : М(ХУ)= М(Х) М(У).

76.Дисперсия случайной величины равна: D(Х)=М[Х –М(Х)]

77.Для дискретной случайной величины дисперсия равна: D(Х) = 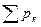[ 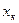-M(Х)] .

78.Среднее квадратическое отклонение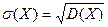

79.Свойства дисперсии. Если С- постоянная величина, то: D(C) = 0

80.Свойства дисперсии. Если к- постоянная величина, то: D(кХ)= к ²- D(Х)

81.Свойства дисперсии. Если С- постоянная величина, то: D(Х+С)=D(Х)

82.Если У – случайная величина, то : D(Х+У) = D(Х) + D(Y)

83.Если У – случайная величина, то : D(X-Y ) = D(Х) +D(Y).

84.Свойства среднего квадратического отклонения. Если С- постоянная величина, то: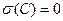

85.Свойства среднего квадратического отклонения. Если С- постоянная величина, то: 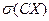=!С!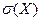

86.Свойства среднего квадратического отклонения. Если С- постоянная величина, то:

87.Случайная величина Х, равная числу наступления события А в п независимых F(испытаниях, в каждом из которых она имеет вероятность р, распределена по биноминальному закону с параметрами n,p. Как мы знаем, Х принимает значения 0, 1, 2,…, п, а соответствующие вероятности задаются формулой Бернулли. Для биноминального распределения имеем: М(Х) = np, D(Х)= npq,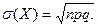

88.Дискретная величина Х, распределенная по закону Пуассона с параметром 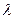,имеет следующие числовые характеристики: М(Х) = 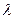, D(Х) = , .

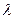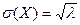Если ее функция распределения всюду непрерывна и имеет производную во всех точках, за исключением, может быть, конечного их числа на каждом конечном интервал называется: называется непрерывной случайной величиной