Кинематика точки

КИНЕМАТИКА

Кинематика точки

Определить движение точки - это значит уметь определить положение точки по отношению к выбранной системе отсчета в любой момент времени.

В кинематике применяются три способа задания движения точки: векторный, координатный и естественный.

При векторном способе определения движения точки радиус-вектор движущейся точки М (рис. 21), проведенный из выбранного неподвижного центра О, выражается как векторная функция от времени, т. е.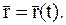

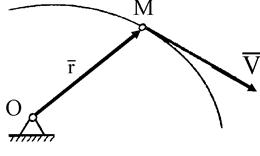Рис. 21

Скорость точки, характеризующая быстроту и направление движения точки, равна производной по времени от ее радиуса-вектора:

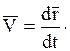
Ускорение 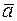точки, характеризующее изменение скорости по модулю и направлению, равно производной по времени от вектора скорости:

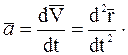
Координатный способ определения (задания) движения точки состоит в том, что координаты движущейся точки в выбранной системе координат выражаются как функции времени t.

Уравнения движения точки в декартовых координатах имеют вид

x = x(t), y = y (t), z = z (t).

Если точка движется в плоскости Оху, то будем иметь только два уравнения движения:

x = x(t), y = y (t).

Для того чтобы найти траекторию точки, достаточно из уравнений движения исключить время t. Вектор скорости и вектор ускорения определяются по их проекциям на оси декартовых координат, причем

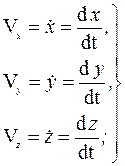
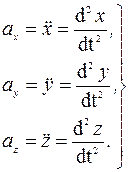
Отсюда получаем формулы разложения векторов скорости и ускорения 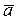по координатным осям:

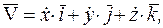
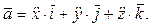
Модули векторов скорости и ускорения вычисляем по формулам

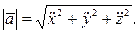
При естественном способе движение точки задается ее траекторией и уравнением движения по этой траектории:

где О - начало отсчета дуг на траектории; s - дуговая координата точки М или взятая с соответствующим знаком длина дуги, отсчитываемая вдоль траектории от начала отсчета до точки М (рис. 22).

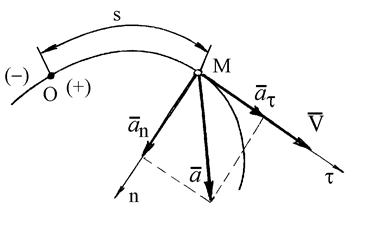
Рис. 22

Если заданы траектория движущейся точки и закон ее движения по этой траектории s = s (t), то вектор скорости направлен по касательной к этой траектории, а его проекция на направление касательной определяется по формуле

причем абсолютное значение этой проекции равно модулю скорости:

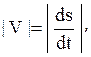
Вектор ускорения определяется по его проекциям на естественные оси (касательную, главную нормаль и бинормаль):

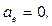
где r - радиус кривизны траектории в данной точке.

Следовательно,

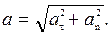
Отметим частные случаи:

1. Если точка движется прямолинейно и неравномерно, то радиус кривизны траектории r ® µ и, следовательно, а_n = 0. В этом случае ускорение направлено вдоль траектории точки и по модулю равно

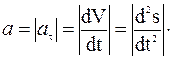
2. Если точка движется по криволинейной траектории равномерно, то

V = const и

и поэтому ускорение направлено по нормали к траектории и по модулю равно

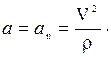
3. Если точка движется прямолинейно и равномерно, то a_n = 0, a_t = 0 и a = 0.

В том случае, когда движение точки задано в координатной форме, касательное ускорение определяется по формуле

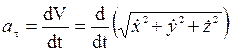, или

После этого нормальное ускорение можно найти из равенства

где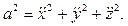

Определив 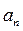, найдем радиус кривизны по формуле

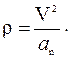
Если плоская траектория задана уравнением у = у(х), то радиус кривизны траектории вычисляется по формуле

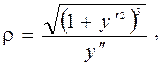
где 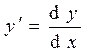и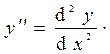

Пример K1. Даны уравнения движения точки в плоскости ху:

x = 6×cos (p×t/6) – 3, y = – 4×cos² (p×t/6)

(х, у - в метрах, t - в секундах).

Определить уравнение траектории точки. Для момента времени t₁ = 1 с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Решение. Для определения траектории исключим из заданных уравнений движения время t, воспользовавшись подстановкой:

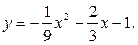
Из полученного выражения следует, что траекторией движения точки является парабола с нисходящими ветвями и осью, параллельной оси у; вершина параболы находится в точке с координатами х = -3 м, у = 0.

Найдем проекции вектора скорости на оси координат:

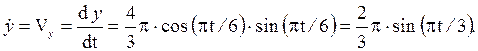
Подставив t₁ = 1 с в полученные выражения, находим

Скорость точки в момент времени t₁ = 1 с

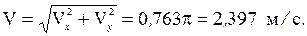
Найдем проекции вектора ускорения:

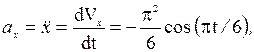
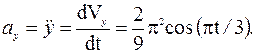
Для момента времени t₁ = 1 с

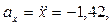
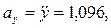
м/с².

Касательное ускорение найдем по формуле

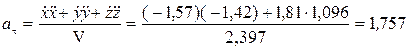м/с².

Нормальное ускорение

м/с².

Вычислим радиус кривизны траектории в том месте, где находится точка в момент времени t₁ = 1 с:

м.

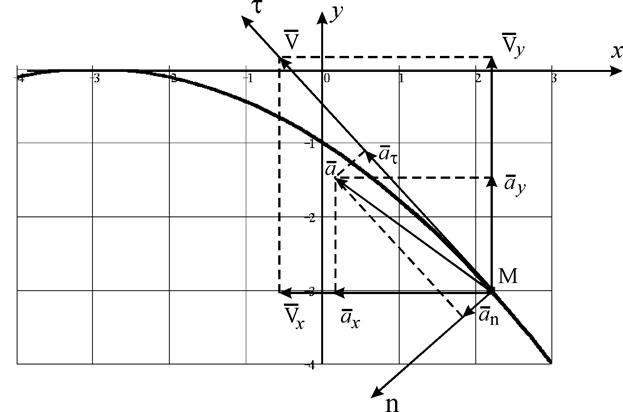
Рис. K1

Пользуясь уравнением траектории, вычерчиваем параболу (рис. K1) и показываем на ней точку М в заданный момент времени по ее координатам. Вектор скорости 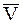строим по составляющим 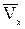и 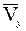; он должен быть направлен по касательной к траектории. Вектор ускорения находим по его составляющим и . Далее найденный вектор раскладываем на направления касательной и нормали и получаем векторы касательного и нормального 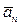ускорений. Полученные таким образом значения и 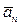должны совпасть с результатами их подсчета по формулам.