Составное (сложное) движение точки

Составное движение точки - это такое движение, при котором точка одновременно участвует в двух или нескольких движениях.

Рассмотрим тело А (рис. 28), которое свободно движется по отношению к неподвижной системе координат О₁x₁y₁z₁. Пусть точка М совершает движение по поверхности этого тела. Через произвольную точку О движущегося тела проведем неизменно связанные с этим телом оси x, y, z. Систему осей Оxyz называют подвижной системой отсчета.

Движение точки М по отношению к неподвижной системе отсчета называют абсолютным движением точки.

Абсолютное движение точки характеризуется изменением радиуса-вектора по модулю и направлению.

Скорость и ускорение точки в абсолютном движении называют абсолютной скоростью и абсолютным ускорением точки и обозначают и .

Рис. 28

Движение точки М по отношению к подвижной системе отсчета называют относительным движением точки. Относительное движение характеризуется изменением только радиуса-вектора 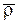при неизменных радиусах-векторах и . В этом случае координаты х, у, z точки М в подвижной системе отсчета будут изменяться.

Скорость и ускорение точки в относительном движении называют относительной скоростью и относительным ускорением и обозначают 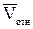и .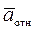

Движение подвижной системы отсчета Оxyz и неизменно связанного с ней тела А по отношению к неподвижной системе отсчета О₁x₁y₁z₁ является для точки М переносным движением. Переносное движение точки М характеризуется изменением радиусов-векторов и по модулю и направлению при неизменном только по модулю радиусе-векторе .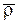

Скорость и ускорение той точки тела А, с которой в данный момент совпадает точка М, называют переносной скоростью и переносным ускорением точки М и обозначают и .

Желая изучить относительное движение точки, следует мысленно остановить переносное движение. Если необходимо изучить переносное движение точки, то надо мысленно остановить относительное движение и рассмотреть далее движение точки по формулам кинематики точки в абсолютном движении.

Если точка М участвует в составном движении, то имеют место следующие теоремы:

абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей точки, т. е.

= + ;

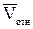абсолютное ускорение точки равно геометрической сумме переносного, относительного и кориолисова (поворотного) ускорений этой точки, т. е.

= + + ,

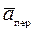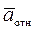или

= + + + + .

Кориолисово ускорение равно удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки, т. е.

= 2 × ( ´ ).

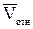Следовательно, модуль этого ускорения

= 2 × w_пер × V_отн × sin a,

где a - угол между векторами и .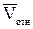

Чтобы найти направление кориолисова ускорения 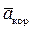точки М, достаточно в точке М построить векторы и 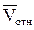и восстановить из этой точки перпендикуляр к плоскости, в которой лежат эти векторы и 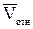. Вектор 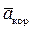направлен по этому перпендикуляру так, чтобы наблюдатель, смотрящий с конца этого вектора, видел поворот вектора на угол a против хода часовой стрелки до совмещения его с вектором 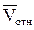(рис. 29).

Рис. 29

Направление вектора 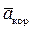можно определить и другим способом (правило Н. Е. Жуковского).

Проведем через точку М плоскость П, перпендикулярную к вектору и спроецируем относительную скорость 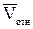на эту плоскость. Если полученную проекцию повернем в плоскости П на 90° вокруг точки М в направлении переносного вращения, то получим направление вектора .

Указания. Задача К3 – на сложное движение точки. Для ее решения воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка М на пластине в момент времени t₁ = 1 с, и изобразить точку именно в этом положении.

Рассмотрим два примера решения этой задачи.

Пример К3а. Пластина OEAB₁D (OE = OD, рис. К3а) вращается вокруг оси, проходящей через точку О перпендикулярно плоскости пластины, по закону j = f₁(t) (положительное направление отсчета угла j показано на рис. К3а дуговой стрелкой). По дуге окружности радиуса R движется точка В по закону s = = f₂(t) (положительное направление отсчета s – от A к B).

Дано: R = 0,5 м, j = t² - 0,5t³, s = p×R×cos(pt/3) (j - в радианах, s - в метрах, t - в секундах). Определить: и в момент времени t₁ = 2 с.

Решение. Рассмотрим движение точки В как сложное, считая ее движение по дуге окружности относительным, а вращение пластины – переносным движением. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам:

= + ,

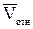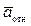= + + , (58)

где, в свою очередь,

= + , = + .

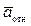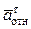Рис. К3а

Определим все входящие в равенства (58) величины.

1. Относительное движение. Это движение происходит по закону

s = = p×R× cos(pt/3). (59)

Сначала установим, где будет находиться точка В на дуге окружности в момент времени t₁. Полагая в уравнении (59) t₁ = 2 с, получаем

s = p×R× cos(2p/3) = - 0,5pR.

Тогда

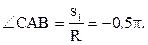
Знак минус свидетельствует о том, что точка В в момент t₁ = 2 с находится справа от точки А. Изображаем ее на рис. К3а в этом положении (точка В₁).

Теперь находим числовые значения , , :

,

,

где r_отн – радиус кривизны относительной траектории, равный радиусу окружности R. Для момента t₁ = 2 с, учитывая, что R = 0,5 м, получаем

м/с,

м/с², м/с². (60)

Знаки показывают, что вектор направлен в сторону положительного отсчета расстояния s, а вектор – в противоположную сторону; вектор направлен к центру С окружности. Изображаем все эти векторы на рис. К3а.

2. Переносное движение. Это движение (вращение) происходит по закону j = t² – 0,5×t³. Найдем сначала угловую скорость w и угловое ускорение e переносного вращения:

= 2×t – 1,5×t², 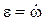= 2 – 3×t;

и при t₁ = 2 с

w = – 2 c^–1, e = – 4 с^–2. (61)

Знаки указывают, что в момент t₁ = 2 с направления w и e противоположны направлению положительного отсчета угла j; отметим это на рис. К3а.

Для определения и находим сначала расстояние h₁ = OB₁точки B₁ от оси вращения О. Из рисунка видно, что h₁ = 2R× 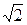= 1,41 м. Тогда в момент времени t₁ = 2 с, учитывая равенства (61), получим

V_пер = |w|×h₁ = 2,82 м/с,

= |e|×h₁ = 5,64 м/с², = w²×h₁ = 5,64 м/с². (62)

Изображаем на рис. К3а векторы и с учетом направлений w и e и вектор (направлен к оси вращения).

3. Кориолисово ускорение. Модуль кориолисова ускорения определяем по формуле а_кор = 2× |V_отн| × |w| × sin a, где a – угол между вектором и осью вращения (вектором ). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор . Численно в момент времени t₁ = 2 с, так как в этот момент |V_отн| = 1,42 м/с и |w| = 2 с^-1, получим

а_кор = 5,68 м/с². (63)

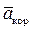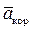Направление найдем по правилу Н. Е. Жуковского: так как вектор лежит в плоскости, перпендикулярной оси вращения, то повернем его на 90° в направлении w, т. е. по ходу часовой стрелки. Изображаем на рис. К3а. (Иначе направление можно найти, учтя, что = 2×( ´ ).

Таким образом, значения всех входящих в правые части равенств (58) векторов найдены и для определения V_абс и а_абс остается только сложить эти векторы. Произведем это сложение аналитически.

4. Определение V_абс. Проведем координатные оси В₁ху(см. рис. К3а) и спроектируем почленно обе части равенства 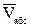= + на эти оси. Получим для момента времени t₁ = 2 с:

V_{абс х} = V_{отн х} + V_{пер х} = 0 - |V_пер| × сos 45° = - 1,99 м/с,

V_{абс у} = V_{отн у} + V_{пер у} = |V_отн| + |V_пер| × сos 45° = 3,41 м/с.

После этого находим

м/с.

Учитывая, что в данном случае угол между и равен 45°, значение V_абс можно еще определить по формуле

м/с.

5. Определение а_абс. По теореме о сложении ускорений

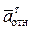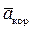= + + + + . (64)

Для определения 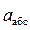спроецируем обе части равенства (64) напроведенные оси В₁ху. Получим:

а_{абс х} = + а_кор + × cos 45° - | |× cos 45°,

а_{абс y} = × cos 45° + | |× cos 45° - | |.

Подставив сюда значения, которые все величины имеют в момент времени t₁ = 2 с, найдем, что в этот момент

а_{абс х} = 9,74 м/с²; а_{абс y} = 7,15 м/с².

Тогда

м/с².

Ответ: V_абс = 3,95 м/с, а_абс = 12,08 м/с².

Пример К3б. Треугольная пластина ADE вращается вокруг оси z по закону j = f₁(t) (положительное направление отсчета угла j показано на рис. К3б дуговой стрелкой). По гипотенузе AD движется точка Впо закону s = АВ = f₂(t); положительное направление отсчета s – от А к D.

Дано: j = 0,1× t³–2,2× t, s = АВ = 2 + 15× t – 3×t²; (j – в радианах, s – в сантиметрах, t – в секундах). Определить: V_абс и а_абс в момент времени t₁ = 2 с.

Решение. Рассмотрим движение точки В как сложное, считая ее движение по прямой AD относительным, а вращение пластины – переносным. Тогда абсолютная скорость 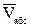и абсолютное ускорение найдутся по формулам:

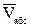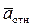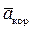= + , = + + , (65)

где, в свою очередь, = + .

Определим все входящие в равенство (65) величины.

1. Относительное движение - это движение прямолинейное и происходит по закону

s = AB = 2 + 15t - 3t², (66)