Поле физической величины

КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

Поле физической величины

Кинематика - раздел механики капельных жидкостей, в котором рас­сматриваются виды и формы движения жидкости без выяснения природы и сил, вызывающих это движение.

Чтобы описать движение жидкости, необходимо задаться определенны­ми свойствами ее в каждой точке (скоростью, давлением, плотностью и др) Непрерывность распределения характеристик в сплошной среде приводит к понятию поля физической величины, под которым понимают часть пространства, в каждой точке которого физическая величина определена однозначно.

Если поле физической величины не зависит от времени, его называв стационарным, или установившимся. Поле физической величины нестационарно, если его параметры зависят от времени.

Поля могут быть скалярных, векторных и тензорных величин. Скалярное поле - поле скалярной величины, или множество:

К скалярам в механике жидкости относятся плотность, давление, температура и др. Значения этих параметров в данной точке и при данных условиях не зависят от выбора системы координат, т. е. скалярные величины инвариантны относительно системы координат.

С целью наглядного представления о поле вводят понятие поверхностей уровня, т. е. таких геометрических мест (в данный момент времени), в которых физическая величина имеет одно и то же значение (изотермы, изобары, изопотенциальные поверхности и др.).

Уравнение поверхности уровня:

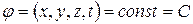
Рисунок 12

Рассмотрим поле физической величины мысленно «расслоив» пространство поверхностями уровня (рис. 12). Внешним пространством по отношению к данной поверхности уровня условимся называть область, где константа С имеет большее значение Нормаль, направленная в сторону возрастания функции (рис. 12), является главной, или внешней, нормалью, направление которой принима­ется за положительное.

Интенсивность поля скалярной величины (функции) определяется ее градиентом grad . Градиент функции есть вектор, направленный по внеш­ней нормали к поверхности уровня и равный по величине производной от этой функции по внешней нормали:

Следовательно, несмотря на то, что скаляры определяются одним веществен­ным значением, изменение их в пространстве характеризуется векторно, т. е. фиксируется направление изменения физической величины. Градиент функ­ции по внешней нормали, по определению производной, есть величина все­гда положительная.

Кроме того, grad , взятый по направлению главной нормали (рис. 12), есть максимальное значение производной от функции.

С векторным полем связаны понятия линий и трубок тока, которые рассмотрим ниже.