Основные виды и формы движения жидкости

При изучении принимается, что жидкость является сплошной средой даже при бесконечно малых объемах. Предположение о сплошности позволяет считать все параметры дви­жущейся жидкости непрерывными и дифференцируемыми функциями коор­динат и времени.

Жидкость состоит из бесконечно боль­шого числа частиц, которые при рас­смотрении уравнений движения физи­чески представляются как очень малая масса жидкости, занимающая соответ­ственно малый объем. В процессе дви­жения жидкости изменяются во време­ни взаимные положения ее частиц и их форма. Деформируемость частицы жид­кости является ее главной кинемати­ческой особенностью как элемента сплошной среды.

Частица жидкости при движении ха­рактеризуется плотностью, ско­ростью и гидродинамическим давлени­ем.

В проекциях на оси координат следует различать составляющие скорости и_х, и_yи и_г, тогда:

Полная производная каждой из со­ставляющих скоростей может быть пред­ставлена в виде:

где 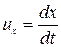, , - проекции скорости ина соответствующие оси, представляющие собой отношение проекции пути на соответствующие оси за время .

Первое слагаемое правой части ра­венства выражает изменение скорости по времени в некоторой фиксированной точке пространства, то есть местное из­менение и поэтому называется локальной производной, или локальной составляющей, ускорения. Остальные слагаемые характеризуют изменение скорости при перемещении частиц жидкости из одной точки пространства в другую и называ­ются конвективными производными, или конвективными составляющими, уско­рения. Конвективное ускорение харак­теризует неоднородность распределе­ния скоростей в точках пространства в данный момент времени.

Гидродинамическое давление р харак­теризует давление в данной точке дви­жущейся жидкости (аналогично гидро­статическому давлению) и по аналогии со скоростью представляет функцию от времени и координат пространства.

Если скорость зависит как от коор­динат точек пространства, так и от вре­мени, то такое движение называется неустановившим­ся, или нестационарным.

Если же скорость зависит только от координат точек пространства и не за­висит от времени (постоянна по вели­чине и направлению в каждой данной точке), то такое движение называется установившимся, или стационарным.

При движении жидкости происходят как перемещение, так и изменение фор­мы (деформация) ее частиц. Различают следующие виды перемещения:

-простое перемещение по направлени­ям хи у(рис. 13, а);

-линейная деформация (растягивание) сторон частицы (рис. 13, б);

-угловая деформация - изменение каж­дого из четырех углов грани (рис.13, в);

-вращение - поворот биссектрисы уг­ла между гранями в том или ином на­правлении (рис.13, г).

Рисунок 13

Различают два вида движения:

-вих­ревое, при котором кроме поступательного движения происходит вращение частиц жидкости вокруг осей, через них проходящих;

-потенциальное, при котором отсут­ствует вращательное движение.

В общем случае компоненты скорости могут быть представлены в та­ком виде:

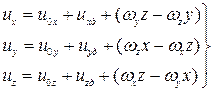
где, координаты х, у, zопределяют центр частицы жидкости в данный мо­мент времени.

Таким образом, движение частицы жидкости слагается из поступательно­го движения центра тяжести частицы со скоростью 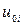, из деформационного движения, обуслов­ленного изменением формы самой час­тицы со скоростями деформации и из вращательного движения с уг­ловыми скоростями .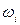

При этом:

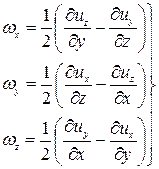
Составляющие скорости деформации частицы в процессе ее движения явля­ются частными производными функ­ции F:

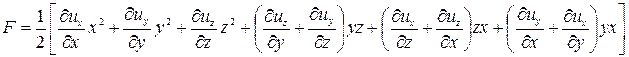то есть .

При движении частиц жидкости раз­личают линию тока, элементарную струйку, вихревую линию и вихревую трубку.

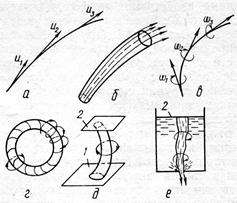
Рисунок 14

Линией тока называется линия, ка­сательная к каждой точке которой в данный момент времени совпадает с направлением вектора скорости (рис. 14, а). Следовательно, линия тока отражает мгновенную картину движе­ния в различных точках. Так как путь частицы жидкости представляет траек­торию ее движения с течением времени, то только в случае установившегося движения линии тока совпадает с траек­ториями движущихся частиц жидкости.

Поверхность, образованная линиями тока, проведенными через все точки бесконечно малого замкнутого кон­тура, называется трубкой тока (рис. 14, б).Масса жидкости, протека­ющей внутри трубки тока, называется элементарной струйкой. Таким обра­зом, элементарную струйку можно рас­сматривать как движущийся бесконечно малый объем жидкости вокруг линии тока. В условиях установившегося дви­жения элементарная струйка обладает свойствами:

-ее форма остается неизменной с течением времени;

-поверх­ность элементарной струйки является непроницаемой, то есть частицы жид­кости не могут войти или выйти через нее;

-вследствие малости поперечного сечения струйки скорости во всех его точках принимаются одинаковыми.

Вихревая линия (рис. 14, в) - это линия, касательная во всех точках к векторам угловой скорости частиц. Вих­ревая линия аналогична линии тока. Поверхность, ограниченная вихревы­ми линиями, проведенными через все точки какого-нибудь бесконечно мало­го простого замкнутого контура, нахо­дящегося в области движущейся жид­кости, называется вихревой трубкой. Вихревая трубка аналогична трубке то­ка. Массу движущейся жидкости внут­ри вихревой трубки называют вихревым шнуром. Вихревой шнур обладает свойствами:

-его сечение нигде не может стать равным нулю, так как в этом сечении скорость вращения долж­на стать бесконечной, что физически не­возможно;

-вихревые шнуры не могут за­канчиваться внутри жидкости - они либо замыкаются на себя, образуя вих­ревые кольца (рис. 14, г),либо «опи­раются» на стенку 1 или свободную по­верхность 2 (рис. 14, д, е).