Два метода кинематического исследования течения жидкости

В гидромеханике существуют два ме­тода изучения движения жидкости: ме­тод Лагранжа и метод Эйлера. Метод Лагранжа заключается в изу­чении движения каждой отдельной частицы жидкости. В этом случае движение определяется положением частицы жид­кости в функции от времени . В началь­ный момент времени ее положение оп­ределено начальными координатами . При движении частица перемеща­ется в новую точку пространства с ко­ординатами . Движение частицы будет определено, если можно установить координаты в заданный момент времени в зависимости от начальных координат :

Эта система уравнений дает возмож­ность построить траектории движения частицы жидкости. Ве­личины являются переменными Лагранжа, а их изменение за время dt позволяет получить значения dx, dy и dz, а затем путь .

Таким образом, метод Лагранжа сво­дится к определению семейства траек­торий движения частиц движущейся жидкости. Метод Лагранжа в гидравлике не на­шел широкого применения ввиду его относительной сложности.

Метод Эйлера основан на изучении поля скоростей под которым понимается вся система векторов, представляю­щих величину и направление скоростей в соответствующих точках пространства, занятого движущейся жидкостью, в дан­ный момент времени. Построение поля скоростей в разных точках для разных моментов времени достаточно полно характеризует дви­жение жидкости.

Переменными Эйлера являются зна­чения скоростей и_х, и_у и и_z, которые определяются в зависимости от коорди­нат точек пространства х, у, z и време­ни t:

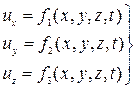
Метод Эйлера нашел широкое при­менение в гидравлике. Он позволяет определить: скорость в любой точке пространства в любой момент времени; скорость в данной точке пространства (х = const, у = const, z= const) с те­чением времени; скорость в фиксиро­ванный момент времени (t = const) в различных точках пространства.