Нахождение расстояния между точками плоскости.

Глава 1. Аналитическая геометрия на плоскости.

Аналитическая геометрия – это область математики, изучающая геометрические задачи средствами алгебры на основе метода координат.

Декартовы прямоугольные система координаты на плоскости

Определяется заданием

· начало координат

· двух взаимно перпендикулярных прямых,

· единицы измерения

· направления роста.

Числовой осью называется прямая, на которой указана начальная точка О, положительное направление и единица длины.

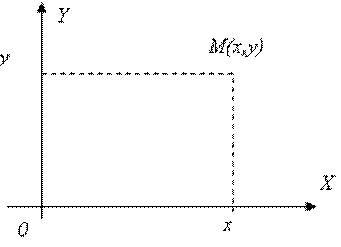
Точка пересечения осей называется началом координат,

а сами оси - координатными осями.

Первая из координатных осей называется осью абсцисс, вторая - осью ординат.

Начало координат обозначается буквой О,

ось абсцисс - символом Ох,

ось ординат - символом Оу.

Сущность метода координат состоит в установлении зависимости между точками и числами.

Нахождение расстояния между точками плоскости.

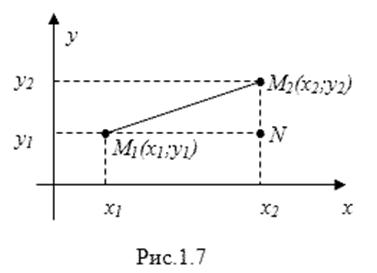
Пусть М₁ (x₁; y₁) и М₂ (x₂; y₂) – некоторые две точки плоскости в декартовой системе координат (рис. 1.7).

Требуется найти формулу, по которой можно было бы находить расстояние |M₁M₂| между этими точками.

Из теоремы Пифагора для треугольника M₁M₂N.

|M₁M₂|² = |M₁N|² + |NM₂|²,

откуда .

Согласно рис. 1.7,

|M₁N| = x₂ – x₁,

|NM₂| = y₂ – y₁.

Поэтому получаем окончательно:

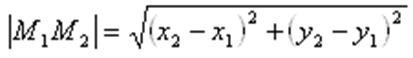
Это и есть та формула, по которой находят расстояние между точками плоскости в декартовой системе координат.

Пример 1. Найти расстояние между точками

А(0;2) и В(4; -1).