Деление отрезка пополам

Задача. Найти координаты середины отрезка

если М – середина отрезка М₁ М₂, то

М₁ М = М М₂

По теореме Фалеса о пропорциональности отрезков прямых, заключенных между параллельными прямыми

А₁ А = АА₂

Следовательно, координаты (x; y) середины отрезка М₁ М₂ таковы:

Деление отрезка в заданном отношении.

Требуется найти точку М, делящую заданный отрезок М₁ М₂ в заданном отношении λ.

Это значит, что искомая точка М должна занимать на отрезке М₁ М₂ такое положение, чтобы выполнялось условие:

По теореме Фалеса:

Но согласно рис. 1.8,

|A₁A| = x – x₁,

|AA₂| = x₂ – x.

Поэтому получаем:

Выражая отсюда x, находим:

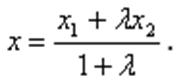
Это – абсцисса искомой точки М.

Совершенно аналогично находим ее ординату y:

Пример 2. Даны точки М₁(-1; 3) и М₂(3; -2). На отрезке М₁М₂ найти точку М(x;y), которая в два раза ближе к М₁, чем к М₂.