II. График гиперболы

I. Определение. Каноническое уравнение.

Опр. Гиперболойназывается геометрическое место точек, разность расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная.

Обозначим: М – производная точка гиперболы;

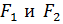– фокусы;

– расстояние между фокусами;

2а – постоянная величина, равная разности расстояний от М до фокусов.

(1) – определение гиперболы

(«+», если ; «–» , если )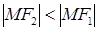

2с>2а 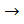с>а (сторона больше разности двух других сторон)

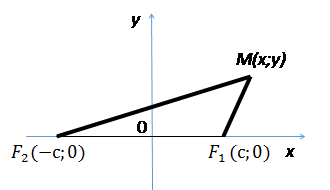Введем прямоугольную систему координат: ось OX проведем через фокусы 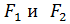, начало координат поместим в середину отрезка . Ось OY через середину 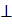OX.

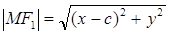
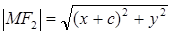
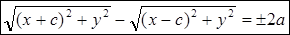(2) – уравнение гиперболы в выбранной системе координат

Преобразовав это уравнение аналогично выводу §3, получим:

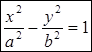(3) – каноническое уравнение гиперболы, где

II. График гиперболы

1. Симметрия.
Гипербола имеет две оси симметрии – ось Ox и ось Oy; и центр симметрии – начало координат O(0;0).