
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Контрольная работа. Задача 2. Общее уравнение прямой на плоскости имеет вид
«АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ»
Задача 2. Общее уравнение прямой на плоскости имеет вид
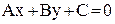 , (1)
, (1)
где А, В – координаты нормального (перпендикулярного) вектора прямой.
Уравнение прямой, проходящей через точку  , перпендикулярно вектору
, перпендикулярно вектору  :
:
 . (2)
. (2)
Уравнение прямой, проходящей через точку  , параллельно вектору
, параллельно вектору  , имеет вид
, имеет вид
 . (3)
. (3)
Уравнение прямой, проходящей через две заданные точки  и
и  :
:
 (4)
(4)
Уравнение прямой, проходящей через данную точку  в данной направлении, имеет вид
в данной направлении, имеет вид
 (5)
(5)
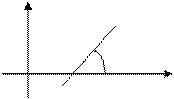
где  - угловой коэффициент прямой,
- угловой коэффициент прямой,  - угол, образованный прямой с положительным направлением на оси ОХ.
- угол, образованный прямой с положительным направлением на оси ОХ.
 у
у

| |
Если прямая проходит через начало координат, то ее уравнение имеет вид
 . (6)
. (6)
Уравнение  (7)
(7)
называется уравнением прямой с угловым коэффициентом, где b – величина отрезка, отсекаемого прямой от оси ОУ.
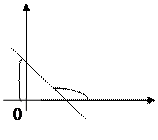
у
b 
х
Пусть две прямые заданы общими уравнениями
 .
.
Если  , то
, то 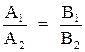 .
.
Если  , то
, то  .
.
Если  , то
, то  .
.
Пусть две прямые заданы уравнениями с угловым коэффициентом
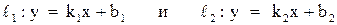 .
.
Если  , то
, то  .
.
Если  , то
, то  .
.
Если  , то
, то 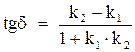 .
.
Расстояние  от точки
от точки  до прямой
до прямой  вычисляется по формуле
вычисляется по формуле
 (8)
(8)
Дата добавления: 2015-04-15; просмотров: 248; Мы поможем в написании вашей работы!; Нарушение авторских прав |