Пример 5. Дано уравнение линии . Записать уравнение линии в нормальной форме и построить эту кривую.

Дано уравнение линии . Записать уравнение линии в нормальной форме и построить эту кривую.

Чтобы привести уравнение к нормальной форме, сгруппируем слагаемые, содержащие только х и у, вынося коэффициенты при за скобки:

.

Дополняем выражения в скобках до полных квадратов:

;

;

;

.

Разделив обе части на 144, получим нормальное уравнение эллипса:

с полуосями с центром в точке . Через точку проведем новые оси координат ( и ) параллельные соответственно осям Ох и Оу. По обе стороны от точки отложим по оси отрезки длиной , а по оси - , получив таким образом вершины эллипса. Проведя через вершины вспомогательные отрезки, параллельные осям, получим прямоугольник, в который нужно вписать эллипс. Чертим эллипс.

у

х

Координаты фокусов эллипса в новых осях: . Здесь . Старыми координатами фокусов будут , т. к. и

Контрольные варианты к задаче 5

Дано уравнение линии . Построить линию, записав это уравнение в нормальной форме. Записать координаты фокусов. Если эта линия окажется пара-

болой, то записать уравнение директрисы.

1. .	2. .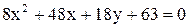
3. .	4. .
5. .	6. .
7. .	8.
9. .	10. .
11. .	12. .
13. .	14. .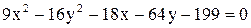
15. .	16. .
17. .	18. .
19. .	20. .
21. 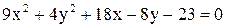.	22. .
23. .	24. .
25. 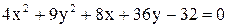.	26. .
27. .	28. .
29. .	30. .