
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретические упражнения
Аналитическая геометрия.
Введение в математический анализ
Индивидуальные задания к модулю 2.1
Курск 2009
УДК 519
Составители: Журавлева Е.В., Фадеева А.Н.
Рецензент
Кандидат физ-мат наук, доцент кафедры
высшей математики В.И. Дмитриев.
Аналитическая геометрия. Введение в математический анализ. [Текст]: /индивидуальные задания к модулю 2.1 системы РИТМо по дисциплине «Математика» / Курск.гос.техн.ун-т; сост.: Е.В. Журавлева, А.Н. Фадеева, Курск, 2009. 36с.: ил. табл. Библиогр.
Приведены индивидуальные задания к модулю 2.1 для студентов экономических специальностей, обучающихся по системе интенсивной рейтинговой технологии модульного обучения. Задания содержат варианты теоретических тестов тренингов, направленных на более внимательное и глубокое изучение тем «Аналитическая геометрия», «Пределы функций», «Непрерывность функций», а также практические упражнения.
Предназначены для студентов экономических специальностей.
Текст печатается в авторской редакции
Подписано в печать ______ . Формат 60х84 1/16.
Усл. печ. л. 0,56. Уч.-изд. л. 0,52. Тираж 50 экз. Заказ ………...
Курский государственный технический университет.
Издательско-полиграфический центр Курского государственного
технического университета. 305040 Курск, ул. 50 лет Октября, 94.
Содержание
Введение. 4
1. Теоретические упражнения. 5
Тест 1. 5
Тест 2. 8
Тест 3. 11
Тест 4. 13
2. Практическая часть. 17
2.1.Задание 1. 17
2.2. Задание 2. 17
2.3. Задание 3. 20
2.4. Задание 4. 21
2.5. Задание 5. 21
2.6. Задание 6. 28
2.7. Задание 7. 30
2.8. Задание 8. 32
Библиографический список. 36
Введение
В современных условиях высшая школа переходит на двухуровневую систему образования. В связи с этим складывается новая концепция образования. Цель учебного процесса заключается не только в передаче знаний от преподавателя к студенту, но и в развитии у студента способности к непрерывному самообразованию, стремлению к пополнению и обновлению знаний, к творческому использованию их на практике, в сферах будущей профессиональной деятельности.
Одной из форм подготовки образованной, творческой и профессионально мобильной личности является самостоятельная работа студентов.
Данная методическая разработка является одним из блоков в модульно – рейтинговой системе дисциплины «Математика». Студентам предлагается выполнить в соответствии со своим вариантом теоретический тест – тренинг, направленный на более глубокое усвоение теоретического материала, и решить предложенные задачи. Защита модуля также включает в себя теоретический блок и практическое решение задач.
Теоретические упражнения
Выполните один из следующих теоретических тестов. Выбор теста осуществляется по формуле: m = mod(n, 4) + 1, где m – номер выполняемого теста, n – номер варианта.
Тест 1
1. Из представленных ниже уравнений укажите общее уравнение прямой на плоскости:
а) y = kx + b б) Ax + By + C = 0
в)  г)
г) 
2. Составьте последовательность действий при выводе канонического уравнения прямой:
а) 
б) даны точка M0(x0, y0), принадлежащая прямой l, и вектор  , ей параллельный
, ей параллельный
в) 
г) составим вектор  , где M(x, y) – текущая точка прямой.
, где M(x, y) – текущая точка прямой.
3. Установите соответствие между уравнением и типом кривой второго порядка:
1)  а) гипербола
а) гипербола
2) 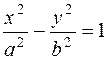 б) парабола, ось симметрии Ох
б) парабола, ось симметрии Ох
3)  в) парабола, ось симметрии Oy
в) парабола, ось симметрии Oy
г) эллипс
4. Для эллипса  укажите два верных утверждения:
укажите два верных утверждения:
а)  б)
б) 
в) директриса  г) асимптота
г) асимптота 
5. Среди представленных ниже уравнений укажите нормальное уравнение плоскости:
а) Аx + By + Cz + D = 0 б) 
в)  г)
г) 
6. Угол между прямой 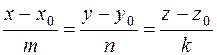 и плоскостью
и плоскостью  находят по формуле:
находят по формуле:
а) 
б) 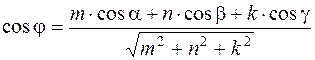
в) 
г)  .
.
7. Сконструируйте определение предела функции f(x) в точке  на языке ε – δ.
на языке ε – δ.
Число a называется пределом функции f(x) в точке  , если функция определена в некоторой окрестности точки
, если функция определена в некоторой окрестности точки  , за исключением, быть может, самой точки
, за исключением, быть может, самой точки  , и
, и

: 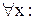

1)  2)
2) 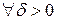 3)
3)  4)
4) 
5)  6)
6)  7)
7)  8)
8) 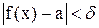
8. Две бесконечно малые функции α(x) и β(x) в точке  являются эквивалентными, если:
являются эквивалентными, если:
а)  б)
б) 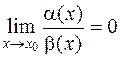
в)  г)
г) 
9. Если функция y = f(x) определена в точке x0 и имеет значение равное f(x0), существуют односторонние пределы равные  и
и  , причем А = B = f(x0), то
, причем А = B = f(x0), то
а)  - точка разрыва первого рода, разрыв устраним;
- точка разрыва первого рода, разрыв устраним;
б)  – точка разрыва второго рода;
– точка разрыва второго рода;
в)  – точка непрерывности;
– точка непрерывности;
г)  – точка разрыва первого рода, разрыв неустраним.
– точка разрыва первого рода, разрыв неустраним.
10. Установите соответствие между графиком функции в окрестности точки  и характером разрыва:
и характером разрыва:
1) 2) 3)



a) точка непрерывности;
б) точка устранимого разрыва;
в) точка неустранимого разрыва;
г) точка разрыва второго рода.
Тест 2
1. Из представленных ниже уравнений укажите каноническое уравнение прямой на плоскости:
а) y = kx + b б) Ax + By + C = 0
в)  г)
г) 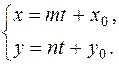
2. Составьте последовательность действий при выводе общего уравнения прямой:
а) 
б) даны точка M0(x0, y0), принадлежащая прямой, и вектор 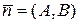 , ей перпендикулярный
, ей перпендикулярный
в) 
где С = -Ax0 – By0.
г) составим вектор  , где M(x, y) – текущая точка прямой.
, где M(x, y) – текущая точка прямой.
3. Установите соответствие между уравнением и типом кривой второго порядка:
1) 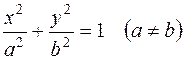 а) гипербола
а) гипербола
2) 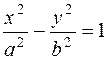 б) парабола, ось симметрии Ох
б) парабола, ось симметрии Ох
3)  в) парабола, ось симметрии Oy
в) парабола, ось симметрии Oy
г) эллипс
4. Для гиперболы  укажите два верных утверждения:
укажите два верных утверждения:
а) асимптота  б)директриса
б)директриса 
в)  г)
г) 
5. Среди представленных ниже уравнений укажите канонические уравнения прямой:
а) Аx + By + Cz + D = 0 б) 
в)  г)
г) 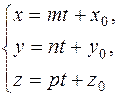
6. Угол между прямой  и плоскостью
и плоскостью  находят по формуле:
находят по формуле:
а) 
б) 
в) 
г)  .
.
7. Сконструируйте определение правостороннего предела функции в точке x0 на языке ε – δ.
Число a называется правосторонним пределом функции f(x) в точке  , если функция определена в некоторой окрестности точки
, если функция определена в некоторой окрестности точки  , за исключением, быть может, самой точки
, за исключением, быть может, самой точки  , и
, и

: 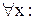

1)  2)
2) 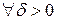 3)
3)  4)
4) 
5)  6)
6)  7)
7) 
8)  9)
9)  10)
10) 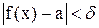
8. Бесконечно малая функция α(x) является функцией более высокого порядка малости, чем бесконечно малая β(x) в точке  , если:
, если:
а)  б)
б) 
в)  г)
г) 
9. Если функция y = f(x) определена в точке x0 и имеет значение равное f(x0), существуют односторонние пределы равные  и
и  , причем А = B ≠ f(x0), то
, причем А = B ≠ f(x0), то
а)  - точка разрыва первого рода, разрыв устраним;
- точка разрыва первого рода, разрыв устраним;
б)  – точка разрыва второго рода;
– точка разрыва второго рода;
в)  – точка непрерывности;
– точка непрерывности;
г)  – точка разрыва первого рода, разрыв неустраним.
– точка разрыва первого рода, разрыв неустраним.
10. Установите соответствие между графиком функции в окрестности точки x0 и характером разрыва:
1) 2) 3)



a) точка непрерывности;
б) точка устранимого разрыва;
в) точка неустранимого разрыва;
г) точка разрыва второго рода.
Тест 3
1. Из представленных ниже уравнений укажите параметрические уравнения прямой на плоскости:
а) y = kx + b б) Ax + By + C = 0
в)  г)
г) 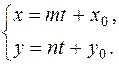
2. Составьте последовательность действий при выводе уравнения прямой на плоскости, проходящей через две различные точки:
а) составим векторы 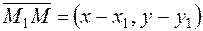 , где M(x, y) – текущая точка прямой, и
, где M(x, y) – текущая точка прямой, и  ;
;
б) даны две точки 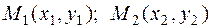 , принадлежащие прямой l;
, принадлежащие прямой l;
в) 
г). 
3. Установите соответствие между уравнением и типом кривой второго порядка:
1)  а) гипербола
а) гипербола
2)  б) парабола, ось симметрии Ох
б) парабола, ось симметрии Ох
3)  в) парабола, ось симметрии Oy
в) парабола, ось симметрии Oy
г) эллипс
4. Для параболы  укажите два верных утверждения:
укажите два верных утверждения:
а) вершина О(0, 0) б) директриса 
в) фокус  г) эксцентриситет e = x0 + 1
г) эксцентриситет e = x0 + 1
5. Среди представленных ниже уравнений укажите общее уравнение плоскости:
а) Аx + By + Cz + D = 0 б) 
в)  г)
г) 
6. Угол между плоскостью Аx + By + Cz + D = 0 и плоскостью  находят по формуле:
находят по формуле:
а) 
б) 
в) 
г) 
7. Дайте определение левостороннего предела функции в точке  на языке ε – δ.
на языке ε – δ.
Число a называется левосторонним пределом функции f(x) в точке  , если функция определена в некоторой окрестности точки
, если функция определена в некоторой окрестности точки  , за исключением, быть может, самой точки
, за исключением, быть может, самой точки  , и
, и

: 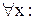

1)  2)
2) 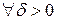 3)
3)  4)
4) 
5)  6)
6)  7)
7) 
8)  9)
9)  10)
10) 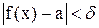
8. Бесконечно малая функция β(x) в точке  является бесконечно малой более высокого порядка малости, чем бесконечно малая α(x), если:
является бесконечно малой более высокого порядка малости, чем бесконечно малая α(x), если:
а)  б)
б) 
в)  г)
г) 
9. Если функция y = f(x) определена в точке x0 и имеет значение равное f(x0), существуют односторонние пределы равные  и
и  , причем А ≠ B, то
, причем А ≠ B, то
а)  - точка разрыва первого рода, разрыв устраним;
- точка разрыва первого рода, разрыв устраним;
б)  – точка разрыва второго рода;
– точка разрыва второго рода;
в)  – точка непрерывности;
– точка непрерывности;
г)  – точка разрыва первого рода, разрыв неустраним.
– точка разрыва первого рода, разрыв неустраним.
10. Установите соответствие между графиком функции в окрестности точки x0 и характером разрыва:
1) 2) 3)



a) точка непрерывности;
б) точка устранимого разрыва;
в) точка неустранимого разрыва;
г) точка разрыва второго рода.
Тест 4
1. Из представленных ниже уравнений укажите уравнение прямой с угловым коэффициентом:
а) y = kx + b; б) Ax + By + C = 0;
в)  ; г)
; г) 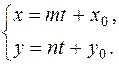
2. Составьте последовательность действий при выводе общего уравнения прямой:
а)  ;
;
б) даны точка M0(x0, y0), принадлежащая прямой, и вектор 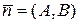 , ей перпендикулярный;
, ей перпендикулярный;
в) 
где С = -Ax0 – By0.
г) составим вектор 
3. Установите соответствие между уравнением и типом кривой второго порядка:
1)  а) гипербола
а) гипербола
2) 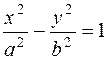 б) парабола, ось симметрии Ох
б) парабола, ось симметрии Ох
3)  в) парабола, ось симметрии Oy
в) парабола, ось симметрии Oy
г) эллипс
4. Для параболы  укажите два верных утверждения:
укажите два верных утверждения:
а) вершина О(0, y0) б) директриса 
в) фокус  г) эксцентриситет e = x0 + 1
г) эксцентриситет e = x0 + 1
5. Среди представленных ниже уравнений укажите параметрические уравнения прямой:
а) Аx + By + Cz + D = 0 б) 
в)  г)
г) 
6. Прямая 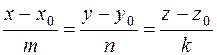 и плоскость
и плоскость  параллельны, если:
параллельны, если:
а) 
б) 
в) 
г) 
7. Дайте определение бесконечно малой функции α(x) в точке x0 на языке ε – δ.
Функция α(x) называется бесконечно малой в точке  , если функция определена в некоторой окрестности точки
, если функция определена в некоторой окрестности точки  , за исключением, быть может, самой точки
, за исключением, быть может, самой точки  , и
, и

: 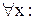

1)  2)
2) 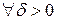 3)
3)  4)
4) 
5)  6)
6)  7)
7) 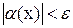 8)
8) 
8. Бесконечно малая функция β(x) в точке  является бесконечно малой одного порядка малости с бесконечно малой α(x), если:
является бесконечно малой одного порядка малости с бесконечно малой α(x), если:
а)  б)
б) 
в)  г)
г) 
9. Если функция y = f(x) определена в точке  и имеет значение равное f(x0), односторонние пределы равны
и имеет значение равное f(x0), односторонние пределы равны  и
и  , то
, то
а)  - точка разрыва первого рода, разрыв устраним;
- точка разрыва первого рода, разрыв устраним;
б)  – точка разрыва второго рода;
– точка разрыва второго рода;
в)  – точка непрерывности;
– точка непрерывности;
г)  – точка разрыва первого рода, разрыв неустраним.
– точка разрыва первого рода, разрыв неустраним.
10. Установите соответствие между графиком функции в окрестности точки  и характером разрыва:
и характером разрыва:
1) 2) 3)



a) точка непрерывности;
б) точка устранимого разрыва;
в) точка неустранимого разрыва;
г) точка разрыва второго рода.
Дата добавления: 2015-04-15; просмотров: 246; Мы поможем в написании вашей работы!; Нарушение авторских прав |