
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задание 2. Составить каноническое уравнение кривой второго порядка (эллипса, гиперболы или параболы) (см
Составить каноническое уравнение кривой второго порядка (эллипса, гиперболы или параболы) (см. табл. 1), расположенной симметрично относительно декартовой системы координат, если … (доп. усл. см. табл. 2). Построить кривую на чертеже и указать на ней фокусы и директрисы (для гиперболы еще и асимптоты) кривой.
Таблица 2.1
Индивидуальные условия к заданию 2.2
| MOD (n, 3) | Кривая | Расположение кривой относительно декартовой прямоугольной системы координат |
| Эллипс | Симметрично относительно начала координат. Фокусы лежат на оси Ox | |
| Гипербола | Симметрично относительно начала координат. Фокусы лежат на оси Ox | |
| Парабола | Симметрично оси Ox. Фокусы лежат на оси Ox |
Таблица 2.2
Дополнительные условия к заданию 2.2
| n | Дополнительные условия |
| Большая полуось a = 3 и фокусы имеют координаты F(±2; 0) | |
| Фокусы имеют координаты F(±5; 0) и расстояние между директрисами равно 6 | |
| фокальный параметр равен 3,5 и парабола лежит в полуплоскости x > 0 | |
| малая полуось b = 2 и уравнение директрисы x = 4 | |
| фокальный параметр p = 5 и действительная полуось a = 6 | |
| уравнение директрисы x = - 1,5 | |
| большая полуось a = 4 и фокальный параметр p = 6 | |
| действительная полуось a = 4 и расстояние между фокусами равно 10 | |
| точка М (-1; 2) принадлежит кривой | |
| фокальные радиусы вершин эллипса, лежащих на оси x, равны 1 и 11 (r1= 1, r2= 11) | |
| фокусы имеют координаты F(±7; 0) и уравнения директрис x = ±4 | |
фокус имеет координаты 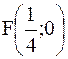
| |
малая полуось 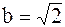 и расстояние между фокусами равно 2 и расстояние между фокусами равно 2
| |
| расстояние между фокусом и соответствующей ему директрисой p = 0,5 и фокусы имеют координаты F(±6; 0) | |
| уравнение директрисы x = 0,25 | |
| расстояние между фокусами равно 4 и расстояние между директрисами равно 6 | |
действительная полуось равна 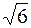 и эксцентриситет равен и эксцентриситет равен 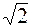
| |
| фокальный параметр p = 1,25 и парабола лежит в полуплоскости x < 0 | |
| фокусы имеют координаты F(±3; 0) и расстояние от фокуса до соответствующей ему директрисы p = 1 |
Продолжение табл. 2.2
| действительная полуось a = 3 и уравнения асимптот y = ± 2x | |
| парабола проходит через точку М (4; 1) | |
большая полуось 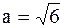 и эксцентриситет равен и эксцентриситет равен 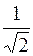
| |
расстояние между директрисами равно 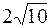 и уравнения асимптот y = ± 3x и уравнения асимптот y = ± 3x
| |
| фокус имеет координаты F(-1; 0) | |
эксцентриситет равен 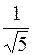 и расстояние между директрисами равно 10 и расстояние между директрисами равно 10
| |
| фокальные радиусы вершин r1= 5, r2= 7 | |
директриса имеет уравнение 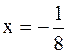
| |
| малая полуось b = 3 и фокальный параметр p = 9 | |
| расстояние между фокусами равно 12 и эксцентриситет равен 0,5 | |
| парабола проходит через точку М (-4; 2) | |
| фокусы имеют координаты F(±2; 0) и эксцентриситет равен 0,5 | |
мнимая полуось 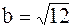 и расстояние между директрисами равно и расстояние между директрисами равно 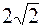
| |
| фокус имеет координаты F(1,5; 0) | |
| расстояние между фокусами равно 4, а расстояние между директрисами равно 6 | |
фокусы имеют координаты F(±3; 0) и уравнения асимптот 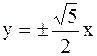
| |
| фокальный параметр равен 3 и парабола расположена в полуплоскости x < 0 | |
уравнения директрис x = ± 4 и фокальный радиус вершин, лежащих на оси y, равен 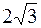
| |
мнимая полуось 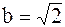 и расстояние между соответствующими друг другу фокусами и директрисами равно 0,5 и расстояние между соответствующими друг другу фокусами и директрисами равно 0,5
| |
| уравнение директрисы x = 1,25 |
Продолжение табл. 2.2
малая полуось b = 2 и эксцентриситет равен 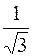
| |
| мнимая полуось b = 2 и фокусы имеют координаты F(±3; 0) | |
| парабола проходит через точку М (1; 4) | |
| большая полуось a = 2 и расстояние между директрисами равно 8 | |
мнимая полуось b = 2 и эксцентриситет равен 
| |
фокус имеет координаты 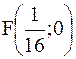
| |
мнимая полуось 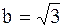 и фокальный радиус вершин эллипса, расположенных на оси Oy, равен и фокальный радиус вершин эллипса, расположенных на оси Oy, равен 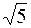
| |
эксцентриситет равен 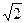 и расстояние между директрисами равно 2 и расстояние между директрисами равно 2
| |
| расстояние между фокусом и директрисой равно 1,5 и парабола расположена в полуплоскости x > 0 | |
эксцентриситет равен 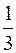 и фокальный радиус вершин эллипса, расположенных на оси Oy, равен 6 и фокальный радиус вершин эллипса, расположенных на оси Oy, равен 6
| |
| мнимая полуось b = 6 и уравнения асимптот y = ± 1,5x |
Дата добавления: 2015-04-15; просмотров: 291; Мы поможем в написании вашей работы!; Нарушение авторских прав |