Задание 5. Вычислить пределы, не пользуясь средствами дифференциального исчисления.

Вычислить пределы, не пользуясь средствами дифференциального исчисления.

Индивидуальные задачи представлены в таблице 2.3.

Таблица 2.3

Индивидуальные задачи к заданию 5

n	а)	б)	в)	г)	д)

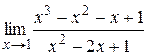
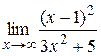
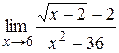
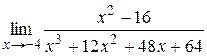
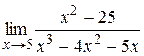
Продолжение табл. 2.3.

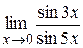
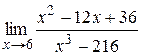
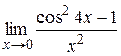
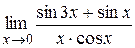
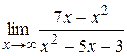
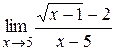
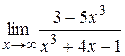
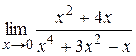
Продолжение табл. 2.3.

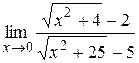
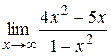
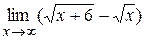
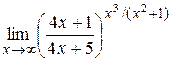
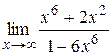
Продолжение табл. 2.3.

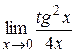
Продолжение табл. 2.3.

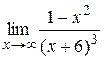
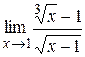
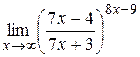
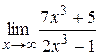
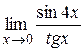
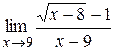
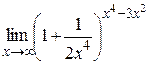
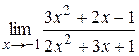
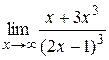
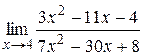
Продолжение табл. 2.3.

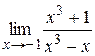
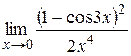
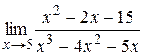
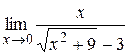
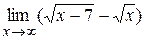
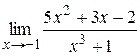
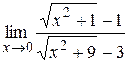
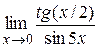
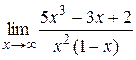
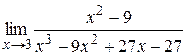
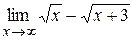
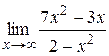
Задание 6

Вычислить односторонние пределы.

Таблица 2.4

Индивидуальные задачи к заданию 6

n	Предел	n	Предел

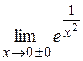
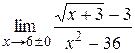
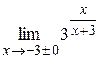
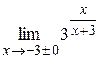
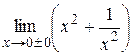
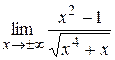
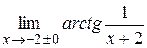
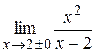
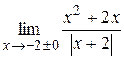
Задание 7

Для функции y = f(x) заданы два значения аргумента x₁ и x₂. Требуется:

1. Установить, является ли данная функция непрерывной при этих значениях аргумента;

2. В случае разрыва установить характер разрыва;

3. Сделать схематический чертеж графика функции.

Индивидуальные задания представлены в табл. 2.5.

Таблица 2.5

Индивидуальные задачи к заданию 7

n	f(x)	x1	x2	n	f(x)	x1	x2
		-1
		-1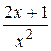
						-1
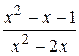
						-1
		-2		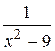		-3
		-1
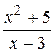
						-2
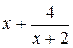
						-2
n	f(x)	x1	x2	n	f(x)	x1	x2
						-2
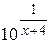
						-4	-2
		-3
		-1
			-1
		-4
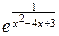
						-3
		-5	-3
						-1
			π
			-1			-7	-7,5
		-1				-3