Кривые безразличия. Их свойства. Кривые безразличия и полезность.

Кривые безразличия – графическое отражение набора потребительских корзин, обеспечивающих потребителю одинаковый уровень полезности. Любая точка на кривой безразличия отражает набор товаров, обеспечивающий одинаковую суммарную полезность, к каждому из этих наборов человек относиться одинаково.

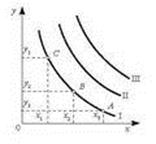
Свойства кривых безразличия:

1. Кривые безразличия не могут пересекаться.

2. Могут быть проведены через любую точку пространства товаров

3. Кривые безразличия имеют отрицательный наклон.

4. Лежащие выше и правее других кривых означают более предпочитаемые наборы товаров

5. Выпуклы к началу координат.

Предельная норма замещения (MRS) — количество, на которое потребление одного из двух благ должно быть увеличено (или уменьшено), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную (предельную) единицу.Предельная норма замещения может принимать различные значения: а) быть равной нулю; б) быть постоянной (для двух полностью взаимозаменяемых товаров); в) меняться при движении вдоль кривой безразличия.

Бюджетное ограничение. Кривые безразличия позволяют выявить потребительские предпочтения. Однако при этом не учитываются два важных обстоятельства: цены товаров и доход потребителей.Эту информацию дает бюджетное ограничение (линия цен, прямая расходов). Бюджетное ограничение показывает, какие потребительские наборы можно приобрести за данную сумму денег.

Если I — доход потребителя, PX — цена блага X, Py — цена блага Y, а X и Y составляют, соответственно, купленные количества благ, то уравнение бюджетного ограничения можно записать следующим образом:

I = PXX + PYY

Проекция поверхности полезности это и есть кривые безразличия. Они соединяют все точки одинаковой совокупности полезности.