Задание № 39

Выборочное уравнение парной регрессии имеет вид y=-3+2x. Тогда выборочный коэффициент корреляции может быть равен …

Варианты ответов: 1) 0,6 2) -0,6 3) -3 4) -2

Решение:

Две случайные величины могут быть связаны между собой функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми.

Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. Если при изменении одной из величин изменяется среднее значение другой, то в этом случае статистическую зависимость называют корреляционной. Значит, корреляционная зависимость есть частный случай статистической зависимости.

Корреляционной зависимостью от называют функциональную зависимость условной средней от :

. (1)

Уравнение (1) называется уравнением регрессии на ; функция называется регрессией на ; график функции - линией регрессии на .

Корреляционной зависимостью от называется функциональная зависимость от :

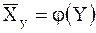. (2)

Уравнение (2) называется уравнением регрессии на ; функция называется регрессией на ; график функции - линией регрессии на .

Наиболее простой и важный случай корреляционной зависимости - линейная регрессия. В этом случае теоретическое уравнение линейной регрессии на (формула (1) имеет вид

. (3)

Коэффициент в уравнении (3) называют коэффициентом регрессии на и обозначают .

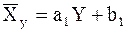Уравнение линейной регрессии на . (4)

Коэффициент называют коэффициентом регрессии на и обозначают .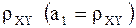

В случае линейной регрессии задача определения тесноты связи сводится к вычислению эмпирического (выборочного) коэффициента корреляции, который можно вычислить по одной из формул:

или , (5)

где - значения средних квадратических отклонений.