Явления переноса в твердых телах

Обсуждается механизм диффузии и теплопроводности в твердых телах. Выясняется смысл энергии активации диффузии. Рассматривается внешняя теплопроводность.

Диффузия. В жидкостях и твердых телах также имеют место явления переноса, но механизм этих явлений отличается от механизма в газах. Это обусловлено тем, что, во-первых, в жидкостях и твердых телах теряет смысл представление о длине свободного пробега и, во-вторых, силы взаимодействия между молекулами очень велики и оказывают постоянное влияние на их движение.

В твердых телах наблюдается как самодиффузия, так и взаимодиффузия. Наиболее наглядно это демонстрируется фактом взаимопроникновения вещества двух тел, находившихся достаточно долгое время в тесном контакте друг с другом.

Самодиффузия осуществляемся главным образом с помощью трех следующих механизмов. Если в узле кристаллической решетки имеется вакансия, то один из соседних атомов может совершить переход из своего узла в вакантный узел. Этот переход эквивалентен движению вакансии. Для того чтобы имел место процесс самодиффузии, обусловленный движением вакансий, необходимо, чтобы в решетке присутствовало неравномерное распределение вакансий, т. е. градиент плотности ва­кансий. При создании вакансий важную роль играют дислокации.

Для осуществления диффузии посредством движения вакансий необходимо одновременное наличие двух условий: существование вакансии и образование у одного из соседних атомов достаточно большой энергии колебаний, чтобы он смог покинуть свой узел. Если у атома в узле кристаллической решетки образовалась достаточно большая энергия колебаний, то он покидает свой узел. Если по соседству нет вакансии, то он располагается между узлами и затем движется в междоузлиях. Может произойти обмен атомами в соседних узлах решетки. Этот механизм диффузии не связан с движением дефектов кристаллической решетки.

Диффузия в твердом теле описывается уравнением Фика, однако коэффи­циент диффузии D определяется другими факторами. Главную роль в диффузии играет движение вакансий. Обозначим: τ — среднее время «оседлой» жизни атома в узле решетки, <d> — смещение атома при перескоке. Ясно, что <d> примерно равно основным периодам кристаллической решетки. Средняя скорость движения атомов при перескоках <v> = <d>/<τ>. Атом может равновероятно сделать перескок <d> по шести независимым направлениям. Следовательно,

D=<v> <d>/6 = (<d>²/(6<τ>). (5.6)

Для осуществления перескока необходимо, чтобы имелась вакансия и соседний атом имел достаточную энергию для совершения перескока в вакансию.

Обозначим ε_В энергию, при приобретении которой атом покидает обязательно свой узел, в результате чего образуется вакансия. В соответствии с распределением Гиббса вероятность образования вакансии равна

P_В = A_B exp[-e_B/(kT)]. (5.7)

С другой стороны, обозначая ε_П энергию, которую должен иметь атом, чтобы совершить перескок в имеющуюся вакансию, можно для вероятности перескока при наличии вакансии написать

P_П (перескок-вакансия) = A_П exp[-e_П/(kT)]. (5.8)

Отсюда для вероятности P того, что одновременно будет иметься вакансия и совершится перескок в эту вакансию) можем написать

P = P_В P_П (перескок-вакансия) = A exp[-(e_B +e_П)/(kT)]= A exp[-W/(kT)],(5.9)

где А = А_ВА_П— постоянная; W— ε_В + ε_П — энергия активации диффузии, определяемая свойствами вещества.

Очевидно, что частота перескоков прямо пропорциональна вероятности перескока, т.е. 1/< τ > = P. Подставляя это выражение для < τ > в формулу (4.1), находим

D = D₀ exp[-W/(kT)], (5.10)

где D₀ = (1/6)(<d>)²A — постоянная, определяемая свойствами вещества.

Коэффициент диффузии в твердых телах очень мал (неизмеримо меньше, чем для газов). Например, для золота он равен 10^-35 м²/с, в то время как для кислорода в атмосфере он равен примерно 10^-5 м²/с.

Теплопроводность. Она осуществляется не тем, что молекулы перемешаются в твердом теле, а посредством взаимодействия между молекулами, в результате кото­рого их тепловое движение приобретает коллективный характер. В результате этого тепловое движение молекул в твердом теле описывается как идеальный газ фононов.

Для описания теплопроводности можно повторить рассуждения о процессах переноса в газах, имея в виду, что вместо движения молекул понимается движение фононов. Для потока теплоты получается формула , а для теплопроводности на основании формулы для коэффициента теплопроводности можно записать выражение

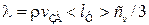, (5.11)

где v_зв — скорость звука в твердом теле; <l_ф> — средняя длина свободного пробега фононов, вычисление которой является не простой задачей. Оно показывает, что <l_ф> = const / Т. Константа определяется свойствами вещества.

Теплопроводность твердых тел во много paз превосходит теплопроводность газов. В то время как теплопроводность газов при нормальных условиях имеет порядок 1 мВт/(м × К), значения теплопроводности твердых тел нередко имеют порядок 1 кВт/(м × К), т. е. в сотни тысяч и миллионы раз больше.

В металлах помимо решеточной теплопроводности необходимо учитывать также и теплопроводность за счет переноса теплоты свободными электронами. Для оценки ее роли необходимо принять во внимание свойства электронного газа.

При высокой температуре электронная теплопроводность очень существенна. Именно ею объясняется высокая теплопроводность металлов по сравнению с неметаллами. При более низкой температуре начинает преобладать решеточная теплопроводность, а при самой низкой температуре, когда решеточная теплопроводность очень мала, снова начинает преобладать электронная теплопроводность.

Внешняя теплопроводность. Если твердое тело окружено средой с другой, чем у тела, температурой, то через поверхность тела идет поток теплоты. Температура на поверхности тела испытывает скачок от температуры Т тела до температуры Т_о среды. Как показывает опыт, при небольших разностях температур Т — Т_о нормальная компонента потока теплоты пропорциональна этой разности:

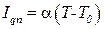, (5.12)

где a — внешняя теплопроводность. Уравнение (4.7) было впервые введено И. Нью­тоном (1701). Коэффициент α находится из эксперимента.

Пример. Найти распределение температуры в сферическом слое тела, внутренняя поверхность которого радиуса r₁ поддерживается при температуре T₁, а внешняя радиуса r₂ — при температуре T₂.

Задача аксиально-симметрична, и поток теплоты направлен по радиусу. В стацио­нарном состоянии тепловой поток сквозь поверхность сферы любого радиуса между r₁ и r₂ постоянен. Следовательно, имеем

. (5.13)

Общее решение этого уравнения

, (5.14)

где А и В — постоянные интегрирования. Они определяются начальными условиями

, ,

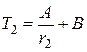откуда , , и решение (5.14) запи­сывается в виде

. (5.15)